Exam 14: Partial Derivatives
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find the directional derivative of the function at the point in the direction of the unit vector that makes the angle with the positive x-axis.
(Multiple Choice)
5.0/5  (42)
(42)
The temperature-humidity index I (or humidex, for short) is the perceived air temperature when the actual temperature is T and the relative humidity is h, so we can write I = f (T, h). The following table of values of I is an excerpt from a table compiled by the National Oceanic and Atmospheric Administration. For what value of T is ? T h \downarrow \rightarrow 20 30 40 50 60 70 80 74 76 78 82 83 86 85 81 82 84 86 90 94 90 86 90 93 96 101 106 95 94 94 98 107 111 125 100 99 101 109 122 129 138
(Short Answer)
4.8/5  (39)
(39)
Two contour maps are shown. One is for a function f whose graph is a cone. The other is for a function g whose graph is a paraboloid. Which is the contour map of a cone? 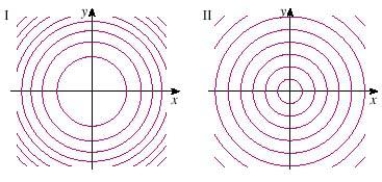
(Multiple Choice)
4.9/5  (40)
(40)
Which of the given points are the points on the hyperboloid where the normal line is parallel to the line that joins the points and .
Select all that apply.
(Multiple Choice)
4.8/5  (30)
(30)
The length l, width w and height h of a box change with time. At a certain instant the dimensions are and , and l and w are increasing at a rate of 10 m/s while h is decreasing at a rate of 1 m/s. At that instant find the rates at which the surface area is changing.
(Short Answer)
4.8/5  (38)
(38)
Find the local maximum, and minimum value and saddle points of the function.
(Short Answer)
4.9/5  (43)
(43)
Use the linearization L(x, y) of the function. at to approximate .
(Short Answer)
4.7/5  (39)
(39)
Use the definition of partial derivatives as limits to find if .
(Multiple Choice)
4.9/5  (31)
(31)
Suppose (1, 1) is a critical point of a function f with continuous second derivatives. In the case of , , what can you say about f ?
(Multiple Choice)
4.9/5  (37)
(37)
The wind-chill index I is the perceived temperature when the actual temperature is T and the wind speed is v so we can write . The following table of values is an excerpt from a table compiled by the National Atmospheric and Oceanic Administration. Use the table to find a linear approximation to the wind chill index function when T is near and v is near 30 kmh.
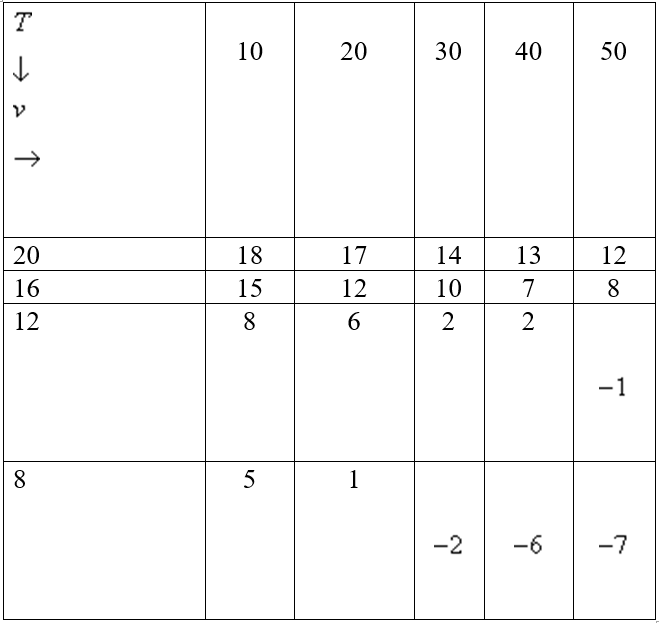
(Short Answer)
4.7/5  (28)
(28)
Showing 41 - 60 of 132
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)