Exam 10: Comparisons Involving Means, Experimental Design, and Analysis of Variance

For four populations, the population variances are assumed to be equal. Random samples from each population provide the following data. Using a .05 level of significance, test to see if the means for all four populations are the same. Show the complete ANOVA table.

Exhibit 10-12 In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). The following information is provided. 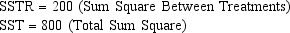-Refer to Exhibit 10-12. The number of degrees of freedom corresponding to between treatments is

Consider the following results for two samples randomly taken from two populations. a.Determine the degrees of freedom for the t distribution. b.Develop a 95% confidence interval for the difference between the two population means.

Consider the following results for two samples randomly taken from two populations. a.Determine the degrees of freedom for the t distribution. b.At 95% confidence, what is the margin of error? c.Develop a 95% confidence interval for the difference between the two population means.

Three universities in your state decided to administer the same comprehensive examination to the recipients of MBA degrees from the three institutions. From each institution, MBA recipients were randomly selected and were given the test. The following table shows the scores of the students from each university. 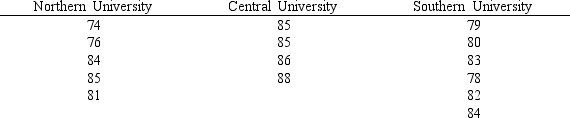a.Compute the overall sample mean. b.At   0.05, test to see if there is any significant difference in the average scores of the students from the three universities. (Note that the sample sizes are not equal.)

Exhibit 10-11 To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. -Refer to Exhibit 10-11. The mean square between treatments (MSTR) equals

If we are testing for the equality of 3 population means, we should use the

Exhibit 10-14 Part of an ANOVA table is shown below. -Refer to Exhibit 10-14. The conclusion of the test is that the means

Exhibit 10-3 A statistics teacher wants to see if there is any difference in the abilities of students enrolled in statistics today and those enrolled five years ago. A sample of final examination scores from students enrolled today and from students enrolled five years ago was taken. You are given the following information. 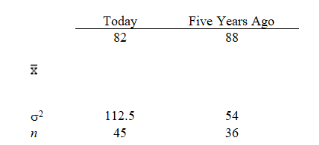-Refer to Exhibit 10-3. What is the conclusion that can be reached about the difference in the average final examination scores between the two classes? (Use a .05 level of significance.)

Consider the following hypothesis test: H₀: ₁  ₂  0 H_a: ₁  ₂  0 The following results are for two independent samples taken from two populations. a.Determine the degrees of freedom for the t distribution. b.Compute the test statistic. c.Determine the p-value and test the above hypotheses.

Exhibit 10-10 A local department store is studying the shopping habits of its customers. They think that the longer customers spend in the store the more they buy. Their study resulted in the following information regarding the amount of time women and men spent in a store. 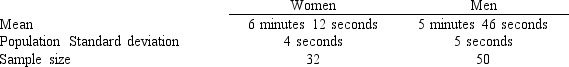-Refer to Exhibit 10-10. The 95% confidence interval for the difference between the two population means is

In ANOVA, which of the following is not affected by whether or not the population means are equal?

A test on world history was given to a group of individuals before and also after a film on the history of the world was presented. The results are given below. We want to determine if the film significantly increased the test scores. (For the following matched samples, let the d  after  before.) 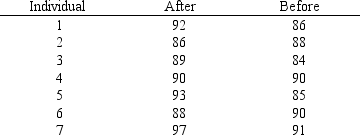a.Give the hypotheses for this problem. b.Compute the test statistic. c.At 95% confidence, test the hypotheses.

Part of an ANOVA table is shown below. 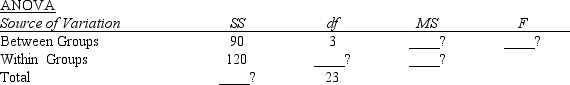a.Determine the missing values and fill in the blanks in the above table. At 95% confidence, test to determine if there is a significant difference among the means. b.How many groups have there been in this problem? c.What has been the total number of observations?

A company attempts to evaluate the potential for a new bonus plan by selecting a sample of 4 salespersons to use the bonus plan for a trial period. The weekly sales volume before and after implementing the bonus plan is shown below. (For the following matched samples, let the difference "d" be d  after  before.) 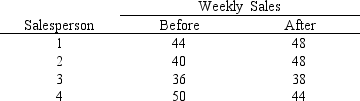a.State the hypotheses. b.Compute the test statistic. c.Use Alpha  .05 and test to see if the bonus plan will result in an increase in the mean weekly sales.

Exhibit 10-1 Salary information regarding male and female employees of a large company is shown below. -Refer to Exhibit 10-1. The point estimate of the difference between the means of the two populations is

The following information regarding the number of semester hours taken from random samples of day and evening students is provided. 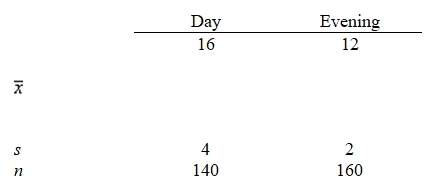Develop a 95% confidence interval estimate for the difference between the mean semester hours taken by the two groups of students.

The following are the results from a completely randomized design consisting of 3 treatments. 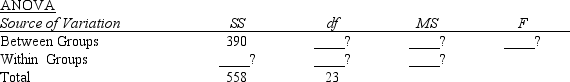Using   .05, test to see if there is a significant difference among the means of the three populations.

Exhibit 10-1 Salary information regarding male and female employees of a large company is shown below. -Refer to Exhibit 10-1. At 95% confidence, the conclusion is the

In an analysis of variance, one estimate of ² is based upon the differences between the treatment means and the