Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Determine whether the matrix is an absorbing stochastic matrix.
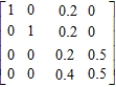
(Short Answer)
4.9/5  (39)
(39)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. 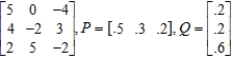
(Multiple Choice)
4.7/5  (29)
(29)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. 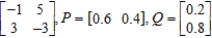
(Multiple Choice)
4.9/5  (39)
(39)
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first, and identify the submatrices R and S. 
(Multiple Choice)
4.7/5  (28)
(28)
Rewrite the absorbing stochastic matrix so that the absorbing states appear first, partition the resulting matrix, and identify the submatrices
R and S. 
(Essay)
4.7/5  (41)
(41)
Find the optimal strategies, P and Q, for the row and column players, respectively. Also compute the expected payoff E of the matrix game and determine which player it favors, if any, if the row and column players use their optimal strategies. 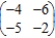
(Multiple Choice)
4.9/5  (24)
(24)
The payoff matrix for a game is  .
Find the expected payoff to the row player if
.
Find the expected payoff to the row player if 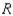 uses the maximin strategy 40% of the time and chooses each of the other two rows 30% of the time, while
uses the maximin strategy 40% of the time and chooses each of the other two rows 30% of the time, while 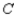 uses the minimax strategy 50% of the time and chooses each of the other columns 25% of the time.
uses the minimax strategy 50% of the time and chooses each of the other columns 25% of the time.
(Multiple Choice)
4.7/5  (37)
(37)
Records compiled by the admissions office at a state of university indicating the percentage of students who change their major each year are shown in the following transition matrix. Of the freshman now at the university, 20% have chosen thier major field as business, 30% in the humanities, 30% in education, and 20% in the natural sciences and other fields. Assuming that this trend continues, find the percentage of these students that will be majoring in each of the given areas in thier senior year. Hint : Find 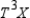 .
Bus)
Hum)
Educ.
Nat) Sc. and others
Business
.
Bus)
Hum)
Educ.
Nat) Sc. and others
Business  Humanities
Education
Nat) sci. and others
Humanities
Education
Nat) sci. and others
(Multiple Choice)
4.9/5  (46)
(46)
Determine whether the given matrix is an absorbing stochastic matrix.
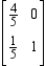
(Short Answer)
4.9/5  (30)
(30)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game.
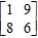
R: row __________C: column __________
R: row __________C: column __________
(Short Answer)
4.9/5  (36)
(36)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given.
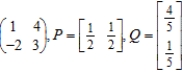
(Essay)
4.7/5  (38)
(38)
Compute the steady-state matrix of the given stochastic matrix. 
(Multiple Choice)
4.8/5  (44)
(44)
Consider the two-person, zero-sum matrix, strictly determined game. 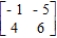
Find the saddle point(s) of the game.
Find the saddle point(s) of the game.
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the given two-person, zero-sum matrix game is strictly determined. 
(Multiple Choice)
4.7/5  (37)
(37)
A study conducted by the Urban Energy Commission in a large metropolitan area indicates the probabilities that homeowners within the area will use certain heating fuels or solar energy during the next 10 years as the major source of heat for their homes. The transition matrix representing the transition probabilities from one state to another is Elec.
Gas)
Oil
Solar
Electricity  Natural gas
Fuel oil
Solar energy
Among homeowners within the area, 35% currently use electricity, 30% use natural gas, 25% use oil, and 10% use solar energy as the major source of heat for their homes. What is the expected distribution of the homeowners that will be using each type of heating fuel or solar energy within the next decade?
Natural gas
Fuel oil
Solar energy
Among homeowners within the area, 35% currently use electricity, 30% use natural gas, 25% use oil, and 10% use solar energy as the major source of heat for their homes. What is the expected distribution of the homeowners that will be using each type of heating fuel or solar energy within the next decade?
(Multiple Choice)
4.9/5  (30)
(30)
Showing 41 - 60 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)