Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
At a certain university, three bookstores - the University Bookstore, the Campus Bookstore, and the Book Mart - currently serve the university community. From a survey conducted at the beginning of the fall quarter, it was found that the University Bookstore and the Campus Bookstore each had 30% of the market, whereas the Book Mart had 40% of the market. Each quarter the University Bookstore retains 80% of its customers, but loses 10% to the Campus Bookstore and 10% to the Book Mart. The Campus Bookstore retains 90% of its customers, but loses 5% to the University Bookstore and 5% to the Book Mart. The Book Mart retains 70% of its customers, but loses 10% to the University Bookstore and 20% to the Campus Bookstore.
What percent of the market will each store have at the beginning of the third quarter?
(Multiple Choice)
4.9/5  (29)
(29)
Compute the steady-state matrix of the given stochastic matrix. 
(Multiple Choice)
4.9/5  (28)
(28)
Determine which of the following is an absorbing stochastic matrix.
(Multiple Choice)
4.7/5  (35)
(35)
The transition matrix for a Markov process and the initial-state distribution vector are given by
State 1 State 2 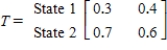 and
and
 Find
Find 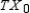 .
.
(Multiple Choice)
4.8/5  (31)
(31)
Determine whether the given two-person, zero-sum matrix game is strictly determined.
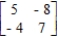
(Essay)
4.7/5  (37)
(37)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game. 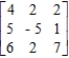
(Multiple Choice)
4.8/5  (29)
(29)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game. 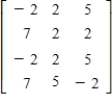

(Short Answer)
4.7/5  (30)
(30)
The registrar of a law school has compiled the following statistics on the progress of the school's students working toward the LLB degree: Of the first-year students in a particular year, 88% successfully complete their course of studies and move on to the second year, whereas 12% drop out of the program; of the second-year students in a particular year, 92% go on to the third year, whereas 8% drop out of the program; of the third-year students in a particular year, 95% go on to graduate at the end of the year, whereas 5% drop out of the program. Determine the probability that a beginning law student enrolled in the program will go on to graduate.
(Multiple Choice)
4.8/5  (31)
(31)
Answer whether the matrix

is the steady-state matrix of the given stochastic matrix
is the steady-state matrix of the given stochastic matrix
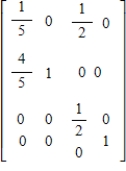
(True/False)
4.7/5  (37)
(37)
As more and more old cars are taken off the road and replaced by late models that use unleaded fuel, the consumption of leaded gasoline will continue to drop. Suppose the transition matrix L UL 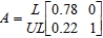 describes this Markov process, where L denotes leaded gasoline and UL denotes unleaded gasoline.
Rewrite the matrix A so that the absorbing states appear first, and identify the submatrices R and S.
describes this Markov process, where L denotes leaded gasoline and UL denotes unleaded gasoline.
Rewrite the matrix A so that the absorbing states appear first, and identify the submatrices R and S.
(Multiple Choice)
4.8/5  (33)
(33)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. 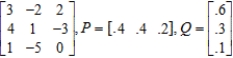
(Multiple Choice)
4.9/5  (42)
(42)
Find the optimal strategies, P and Q, for the row and column players, respectively. Also compute the expected payoff E of the matrix game and determine which player it favors, if any, if the row and column players use their optimal strategies. 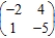
(Multiple Choice)
4.8/5  (36)
(36)
As more and more people switch to broadband Internet service, the demand for dial-up Internet service will continue to drop. Suppose the transition matrix B D 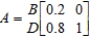 describes this Markov process, where B denotes broadband Internet services and D denotes dial-up Internet service. Compute the steady-state matrix of A.
describes this Markov process, where B denotes broadband Internet services and D denotes dial-up Internet service. Compute the steady-state matrix of A.
(Multiple Choice)
4.8/5  (30)
(30)
Determine which of the following is an absorbing stochastic matrix.
(Multiple Choice)
4.9/5  (25)
(25)
The payoff matrix for a game is

Find the expected payoff to the row player if the row player R uses the maximin pure strategy and the column player C uses the minimax pure strategy.
Find the expected payoff to the row player if R uses the maximin strategy 40% of the time and chooses each of the other two rows 30% of the time, while C uses the minimax strategy 50% of the time and chooses each of the other columns 25% of the time.
Which of these strategies favors the row player?
Find the expected payoff to the row player if the row player R uses the maximin pure strategy and the column player C uses the minimax pure strategy.
Find the expected payoff to the row player if R uses the maximin strategy 40% of the time and chooses each of the other two rows 30% of the time, while C uses the minimax strategy 50% of the time and chooses each of the other columns 25% of the time.
Which of these strategies favors the row player?
(Essay)
4.7/5  (26)
(26)
Find 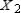 (the probability distribution of the system after two observations) for the given distribution vector
(the probability distribution of the system after two observations) for the given distribution vector 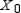 and the given transition matrix
and the given transition matrix 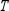 .
.
(Essay)
4.8/5  (31)
(31)
Consider the two-person, zero-sum matrix, strictly determined game.
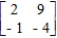
Find the saddle point(s) of the game.
Find the optimal strategy for each player.
R: row __________C: column __________
Find the value of the game.
Determine whether the game favors one player over the other.
Find the saddle point(s) of the game.
Find the optimal strategy for each player.
R: row __________C: column __________
Find the value of the game.
Determine whether the game favors one player over the other.
(Short Answer)
4.9/5  (25)
(25)
Showing 61 - 80 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)