Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
A television poll was conducted among regular viewers of the national news in a certain region where the three national networks share the same time slot for the evening news. Results of the poll indicate that 40% of the viewers watch the ABC evening news, 40% watch the CBS evening news, and 20% watch the NBC evening news. Furthermore, it was found that of those viewers who watched the ABC evening news during 1 week, 75% would again watch the ABC evening news during the next week, 10% would watch the CBS news, and 15% would watch the NBC news. Of those viewers who watched the CBS evening news during 1 week, 80% would again watch the CBS evening news during the next week, 5% would watch the ABC news, and 15% would watch the NBC news. Of those viewers who watched the NBC evening news during 1 week, 80% would again watch the NBC news during the next week, 10% would watch ABC, and 10% would watch CBS. What share of the audience will each network command in the long run?
Please round your answers to the nearest tenth of a percent, if necessary.
__________ % would watch the ABC news
__________ % would watch the CBS news
__________ % would watch the NBC news
(Essay)
4.8/5  (29)
(29)
Consider the two-person, zero-sum matrix, strictly determined game.

Find the saddle point(s) of the game.
Find the optimal strategy for each player.
R: row __________ C: column __________
Find the value of the game.
Determine whether the game favors one player over the other.
Find the saddle point(s) of the game.
Find the optimal strategy for each player.
R: row __________ C: column __________
Find the value of the game.
Determine whether the game favors one player over the other.
(Short Answer)
4.8/5  (38)
(38)
Find the steady-state vector for the transition matrix. 
(Multiple Choice)
4.7/5  (35)
(35)
Find the optimal strategies, P and Q, for the row and column players, respectively. Also compute the expected payoff E of the matrix game and determine which player it favors, if any, if the row and column players use their optimal strategies. 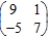
(Multiple Choice)
4.9/5  (45)
(45)
Consider the coin-matching game played by Richie and Chuck with the payoff matrix 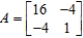
Find the optimal strategies for Richie and Chuck.
Find the optimal strategies for Richie and Chuck.
(Multiple Choice)
4.9/5  (38)
(38)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game.

R: row __________ C: column __________
R: row __________ C: column __________
(Short Answer)
4.8/5  (37)
(37)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game. 
(Multiple Choice)
4.8/5  (40)
(40)
Determine whether the statement is true or false. To find the steady-state distribution vector X, we solve the system 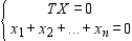
Where T is the regular stochastic matrix associated with the Markov process and
Where T is the regular stochastic matrix associated with the Markov process and
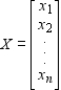
(Not Answered)
This question doesn't have any answer yet
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. 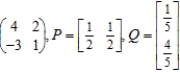
(Multiple Choice)
4.9/5  (28)
(28)
The proprietor of Belvedere's is faced with the problem of deciding whether to expand his restaurant facilities now or to wait until some future date to do so. If he expands the facilities now and the economy experiences a period of growth during the coming year, he will make a net profit of $369,000; if he expands now and a period of zero growth follows, then he will make a net profit of $90,000; and if he expands now and an economic recession follows, he will suffer a net loss of $100,000. If he does not expand the restaurant now and the economy experiences a period of growth during the coming year, he will make a net profit of $257,000; if he does not expand now and a period of zero growth follows, he will make a net profit of $190,000. Finally, if he does not expand now and an economic recession follows, he will make a net profit of $160,000.
Represent this information in the form of a payoff matrix.
Hint: The row player is the proprietor of restaurant and the column player is the economy.
(Multiple Choice)
4.8/5  (43)
(43)
-Find 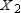 (the probability distribution of the system after two observations) for the given distribution vector
(the probability distribution of the system after two observations) for the given distribution vector 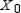 and the given transition matrix
and the given transition matrix 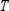 . (Round the answers to three decimal places.)
. (Round the answers to three decimal places.) 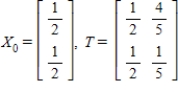
(Multiple Choice)
4.8/5  (37)
(37)
The management of Acrosonic is faced with the problem of deciding whether to expand the production of its line of electrostatic loudspeaker systems. It has been estimated that an expansion will result in an annual profit of $200,000 for Acrosonic if the general economic climate is good. On the other hand, an expansion during a period of economic recession will cut its annual profit to $100,000. As an alternative, Acrosonic may hold the production of its electrostatic loudspeaker systems at the current level and expand its line of conventional loudspeaker systems. In this event, the company is expected to make a profit of $40,000 in an expanding economy (because many potential customers will be expected to buy electrostatic loudspeaker systems from other competitors) and a profit of $170,000 in a recessionary economy.
Should management recommend expanding the company's line of electrostatic loudspeaker systems?
Hint: The row player is the management of the company and the column player is the economy.
(Multiple Choice)
4.8/5  (29)
(29)
Diane has decided to play the following game of chance. She places a $1 bet on each repeated play of the game in which the probability of her winning $1 is 0.3. She has further decided to continue playing the game until she has either accumulated a total of $3 or has lost all her money.
What is the probability that Diane will eventually leave the game a winner if she started with a capital of $2?
(Multiple Choice)
4.8/5  (39)
(39)
Within a large metropolitan area, 10% of the commuters currently use the public transportation system, whereas the remaining 90% commute via automobile. The city has recently revitalized and expanded its public transportation system. It is expected that 6 months from now 10% of those who are now commuting to work via automobile will switch to public transportation, and 90% will continue to commute via automobile. At the same time, it is expected that 40% of those now using public transportation will commute via automobile, and 60% will continue to use public transportation. In the long run, what percent of the commuters will be using public transportation?
(Multiple Choice)
4.9/5  (39)
(39)
The transition matrix for a Markov process and the initial-state distribution vector are given by State 1 State 2  and
and 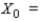
State 1
State 1 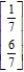
State 2
Find
State 2
Find 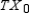 .
.
(Multiple Choice)
4.8/5  (42)
(42)
Determine whether the two-person, zero-sum matrix game is strictly determined. 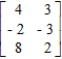 If the game is strictly determined, find the saddle point(s) of the game.
Find the optimal strategy for each player.
If the game is strictly determined, find the saddle point(s) of the game.
Find the optimal strategy for each player.  Find the value of the game.
Determine whether the game favors one player over the other.
The game favors __________ player.
Find the value of the game.
Determine whether the game favors one player over the other.
The game favors __________ player.
(Short Answer)
4.8/5  (37)
(37)
Determine whether the statement is true or false.
The sum of the entries in each column of a transition matrix must not exceed 1.
(Multiple Choice)
4.9/5  (31)
(31)
Find 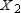 (the probability distribution of the system after two observations) for the distribution vector
(the probability distribution of the system after two observations) for the distribution vector 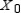 and the transition matrix
and the transition matrix 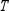 .
. 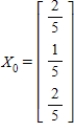
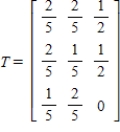
(Multiple Choice)
4.7/5  (33)
(33)
Showing 81 - 100 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)