Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Robin and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1,2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Robin receives an amount in dollars equal to that sum from Cathy. If the sum of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Robin.
Find the minimax and maximin strategies for Robin and Cathy, respectively.
(Multiple Choice)
4.9/5  (36)
(36)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. Give your answer to two decimal places, if necessary.
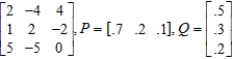
(Short Answer)
4.9/5  (36)
(36)
Diane has decided to play the following game of chance. She places a $1 bet on each repeated play of the game in which the probability of her winning $1 is 0.7. She has further decided to continue playing the game until she has either accumulated a total of $4 or has lost all her money.
What is the probability that Diane will eventually leave the game a winner if she started with a capital of $1?
What is the probability that Diane will eventually leave the game a winner if she started with a capital of $2?
What is the probability that Diane will eventually leave the game a winner if she started with a capital of $3?
Write your answer as a decimal rounded to two decimal places.
(Essay)
4.9/5  (37)
(37)
Find the optimal strategies, P and Q, for the row and column players, respectively. Also compute the expected payoff E of the matrix game and determine which player it favors, if any, if the row and column players use their optimal strategies. 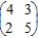
(Multiple Choice)
4.8/5  (39)
(39)
Diane has decided to play the following game of chance. She places a $1 bet on each repeated play of the game in which the probability of her winning $1 is 0.5. She has further decided to continue playing the game until she has either accumulated a total of $4 or has lost all her money.
What is the probability that Diane will eventually leave the game a winner if she started with a capital of $3?
(Multiple Choice)
4.9/5  (43)
(43)
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first, partition the resulting matrix, and identify the submatrices R and S. 
(Multiple Choice)
4.9/5  (36)
(36)
At the beginning of 1990, the population of a certain state was 56.8% rural and 43.2% urban. Based on past trends, it is expected that 20% of the population currently residing in the rural areas will move into the urban areas, while 18% of the population currently residing in the urban areas will move into the rural areas in the next decade. What was the population distribution in that state at the beginning of 2000? Round your answers to the nearest thousandth.
__________ % rural
__________ % urban
(Essay)
4.9/5  (39)
(39)
At a certain university, three bookstores - the University Bookstore, the Campus Bookstore, and the Book Mart - currently serve the university community. From a survey conducted at the beginning of the fall quarter, it was found that the University Bookstore and the Campus Bookstore each had 40% of the market, whereas the Book Mart had 20% of the market. Each quarter the University Bookstore retains 80% of its customers, but loses 5% to the Campus Bookstore and 15% to the Book Mart. The Campus Bookstore retains 90% of its customers, but loses 5% to the University Bookstore and 5% to the Book Mart. The Book Mart retains 70% of its customers, but loses 5% to the University Bookstore and 25% to the Campus Bookstore.
If these trends continue, what percent of the market will each store have at the beginning of the second quarter?  What percent of the market will each store have at the beginning of the third quarter?
What percent of the market will each store have at the beginning of the third quarter?
(Short Answer)
4.7/5  (37)
(37)
Find 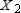 (the probability distribution of the system after two observations) for the given distribution vector
(the probability distribution of the system after two observations) for the given distribution vector 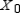 and the given transition matrix
and the given transition matrix 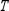 .
. 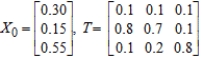
(Multiple Choice)
4.9/5  (42)
(42)
Answer whether the matrix
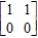
is the steady-state matrix of the given stochastic matrix
is the steady-state matrix of the given stochastic matrix

(True/False)
4.8/5  (31)
(31)
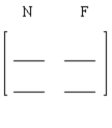
Two dentists, Lydia Russell and Jerry Carlton, are planning to establish practices in a newly developed community. Both have allocated approximately the same total budget for advertising in the local newspaper and for the distribution of fliers announcing their practices. Because of the location of their offices, Russell is expected to get 47% of the business if both dentists advertise only in the local newspaper; if both dentists advertise through fliers, then Russell is expected to get 44% of the business; if Russell advertises exclusively in the local newspaper and Carlton advertises exclusively through fliers, then Russell is expected to get 61% of the business. Finally, if Russell advertises through fliers exclusively and Carlton advertises exclusively in the local newspaper, then Russell is expected to get 50% of the business.
Construct the payoff matrix for the game. 
 C = Carlton; R = Russell
N = local newspaper; F = flyer
C = Carlton; R = Russell
N = local newspaper; F = flyer 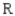
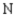
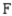 Is the game strictly determined?
Find the optimal strategy for both Russell and Carlton.
Please round the answer to the nearest hundredth.
Is the game strictly determined?
Find the optimal strategy for both Russell and Carlton.
Please round the answer to the nearest hundredth. 
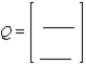
(Essay)
4.9/5  (35)
(35)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game.
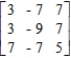
R: row __________ C: column __________
R: row __________ C: column __________
(Short Answer)
4.9/5  (35)
(35)
The payoff matrix for a game is given by 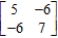
Compute the expected payoff of the game for the pair of strategies.
Compute the expected payoff of the game for the pair of strategies.
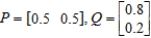
(Multiple Choice)
4.9/5  (32)
(32)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game. 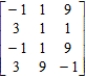
(Multiple Choice)
4.8/5  (39)
(39)
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first, and identify the submatrices R and S. 
(Multiple Choice)
4.9/5  (31)
(31)
Find the optimal strategies, P and Q, for the row and column players, respectively. Also compute the expected payoff E of the matrix game and determine which player it favors, if any, if the row and column players use their optimal strategies. 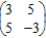
(Multiple Choice)
4.8/5  (34)
(34)
Showing 181 - 200 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)