Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Answer whether the matrix
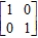
is the steady-state matrix of the given stochastic matrix
is the steady-state matrix of the given stochastic matrix

(True/False)
4.7/5  (34)
(34)
Consider the two-person, zero-sum matrix, strictly determined game. 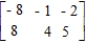
Find the value of the game.
Find the value of the game.
(Multiple Choice)
4.9/5  (42)
(42)
From data compiled over a 10-yr period by Manpower, Inc., in a statewide study of married couples in which at least one spouse was working, the following transition matrix was constructed. It gives the transitional probabilities for one and two wage earners among married couples.  At the present time, 48% of the married couples (in which at least one spouse is working) have one wage earner, and 52% have two wage earners. Assuming that this trend continues, what will be the distribution of one- and two-wage earner families among married couples in this area 10 years from now? Over the long run?
Please round the answers to one decimal place.
Percentage of one-wage earner families among married couples 10 years from now is __________%
Percentage of two-wage earner families among married couples 10 years from now is __________%
Percentage of one-wage earner families among married couples over the long run is __________%
Percentage of two-wage earner families among married couples over the long run is __________%
At the present time, 48% of the married couples (in which at least one spouse is working) have one wage earner, and 52% have two wage earners. Assuming that this trend continues, what will be the distribution of one- and two-wage earner families among married couples in this area 10 years from now? Over the long run?
Please round the answers to one decimal place.
Percentage of one-wage earner families among married couples 10 years from now is __________%
Percentage of two-wage earner families among married couples 10 years from now is __________%
Percentage of one-wage earner families among married couples over the long run is __________%
Percentage of two-wage earner families among married couples over the long run is __________%
(Essay)
4.7/5  (39)
(39)
Determine which of the given matrices is an absorbing stochastic matrix.
(Multiple Choice)
4.7/5  (31)
(31)
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first, and identify the submatrices R and S.

(Essay)
4.9/5  (38)
(38)
To keep track of the location of its cabs, Zephyr Cab has divided a town into three zones: zone I, zone II, and zone III. Zephyr's management has determined from company records that of the passengers picked up in zone I, 40% are discharged in the same zone, 50% are discharged in zone II, and 10% are discharged in zone III. Of those picked up in zone II, 10% are discharged in zone I, 70% are discharged in zone II, and 20% are discharged in zone III. Of those picked up in zone III, 10% are discharged in zone I, 10% are discharged in zone II, and 80% are discharged in zone III. If the initial distribution vector for the location of the taxis is
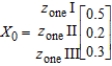
what will be the distribution after all of them have made one pickup and discharge?
__________ %
__________ %
__________ %
what will be the distribution after all of them have made one pickup and discharge?
__________ %
__________ %
__________ %
(Short Answer)
4.8/5  (40)
(40)
The payoff matrix for a game is
 .
Find the expected payoff to the row player if the row player R uses the maximin pure strategy and the column player C uses the minimax pure strategy.
Find the expected payoff to the row player if R uses the maximin strategy 50% of the time and chooses each of the other two rows 25% of the time, while C uses the minimax strategy 60% of the time and chooses each of the other columns 20% of the time.
Which of these strategies favors the row player?
.
Find the expected payoff to the row player if the row player R uses the maximin pure strategy and the column player C uses the minimax pure strategy.
Find the expected payoff to the row player if R uses the maximin strategy 50% of the time and chooses each of the other two rows 25% of the time, while C uses the minimax strategy 60% of the time and chooses each of the other columns 20% of the time.
Which of these strategies favors the row player?
(Essay)
4.9/5  (32)
(32)
Find the steady-state vector for the transition matrix. 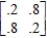
(Multiple Choice)
4.8/5  (30)
(30)
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first, and identify the submatrices R and S.

(Essay)
4.8/5  (37)
(37)
The transition matrix for a Markov process is given by State
1 2 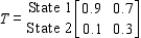 Given that the outcome state 1 has occurred, what is the probability that the next outcome of the experiment will be state 2?
Given that the outcome state 1 has occurred, what is the probability that the next outcome of the experiment will be state 2?
(Multiple Choice)
4.9/5  (35)
(35)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game. 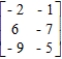
(Multiple Choice)
4.9/5  (25)
(25)
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first, and identify the submatrices R and S.

(Essay)
4.8/5  (37)
(37)
Compute the steady-state matrix of the given stochastic matrix. 
(Multiple Choice)
4.8/5  (37)
(37)
Rewrite the absorbing stochastic matrix so that the absorbing states appear first, partition the resulting matrix, and identify the submatrices R and S.
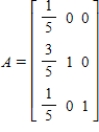
(Essay)
4.8/5  (32)
(32)
The payoff matrix for a game is given by
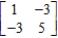
Compute the expected payoffs of the game for the pairs of strategies in the following strategies.
(a)
Compute the expected payoffs of the game for the pairs of strategies in the following strategies.
(a) 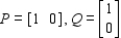
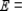 __________
(b)
__________
(b) 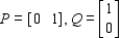
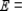 __________
(c)
__________
(c) 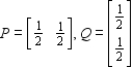
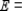 __________
(d)
__________
(d) 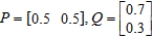
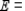 __________
(e) Which of these strategies is most advantageous to R?
__________
(e) Which of these strategies is most advantageous to R?
(Essay)
5.0/5  (35)
(35)
Determine whether the two-person, zero-sum matrix game is strictly determined. 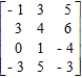 If the game is strictly determined, find the saddle point(s) of the game.
Find the optimal strategy for each player.
Find the value of the game.
Determine whether the game favors one player over the other.
The game favors __________ player.
If the game is strictly determined, find the saddle point(s) of the game.
Find the optimal strategy for each player.
Find the value of the game.
Determine whether the game favors one player over the other.
The game favors __________ player.
(Short Answer)
4.7/5  (33)
(33)
Showing 21 - 40 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)