Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Answer whether the matrix
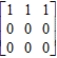
is the steady-state matrix of the given stochastic matrix
is the steady-state matrix of the given stochastic matrix

(True/False)
4.7/5  (40)
(40)
Bella Robinson and Steve Carson are running for a seat in the U.S. Senate. If both candidates campaign only in the major cities of the state, then Robinson is expected to get 60% of the votes; if both candidates campaign only in the rural areas, then Robinson is expected to get 54% of the votes; if Robinson campaigns exclusively in the city and Carson campaigns exclusively in the rural areas, then Robinson is expected to get 40% of the votes; finally, if Robinson campaigns exclusively in the rural areas and Carson campaigns exclusively in the city, then Robinson is expected to get 46% of the votes.
Find the optimal strategy for both Robinson and Carson.
(Multiple Choice)
4.9/5  (30)
(30)
Morris Polling conducted a poll 6 months before an election in a state in which a Democrat and a Republican were running for governor and found that 80% of the voters intended to vote for the Republican and 20% intended to vote for the Democrat. In a poll conducted 3 months later, it was found that 60% of those who had earlier stated a preference for the Republican candidate still maintained that preference, whereas 40% of these voters now preferred the Democratic candidate. Of those who had earlier stated a preference for the Democrat, 70% still maintained that preference, whereas 30% now preferred the Republican candidate.
If the election were held at this time, who would win?
Assuming that this trend continues, which candidate is expected to win the election?
(Multiple Choice)
4.8/5  (37)
(37)
Find the steady-state vector for the transition matrix. 
(Multiple Choice)
4.8/5  (35)
(35)
Find the steady-state vector for the transition matrix. 
(Multiple Choice)
4.9/5  (32)
(32)
The registrar of a law school has compiled the following statistics on the progress of the school's students working toward the LLB degree: Of the first-year students in a particular year, 85% successfully complete their course of studies and move on to the second year, whereas 15% drop out of the program; of the second-year students in a particular year, 92% go on to the third year, whereas 8% drop out of the program; of the third-year students in a particular year, 98% go on to graduate at the end of the year, whereas 2% drop out of the program.
Construct the transition matrix associated with the Markov process.
Please round the answers to the nearest thousandth, if necessary.

Find the steady-state matrix.
Find the steady-state matrix.

Determine the probability that a beginning law student enrolled in the program will go on to graduate.
Determine the probability that a beginning law student enrolled in the program will go on to graduate.
(Essay)
4.9/5  (40)
(40)
Determine whether the statement is true or false.
To find the steady-state distribution vector X, we solve the system
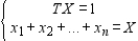
where T is the regular stochastic matrix associated with the Markov process and
where T is the regular stochastic matrix associated with the Markov process and
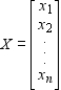
(True/False)
4.9/5  (37)
(37)
Find the optimal strategies, P and Q, for the row and column players, respectively. Also compute the expected payoff E of the matrix game and determine which player it favors, if any, if the row and column players use their optimal strategies. 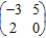
(Multiple Choice)
4.7/5  (32)
(32)
In a study of the domestic market share of the three major automobile manufacturers 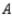 ,
, 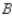 , and
, and 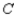 in a certain country, it was found that of the customers who bought a car manufactured by
in a certain country, it was found that of the customers who bought a car manufactured by 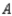 , 70% would again buy a car manufactured by
, 70% would again buy a car manufactured by 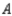 , 10% would buy a car manufactured by
, 10% would buy a car manufactured by 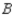 , and 20% would buy a car manufactured by
, and 20% would buy a car manufactured by 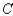 . Of the customers who bought a car manufactured by
. Of the customers who bought a car manufactured by 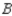 , 80% would again buy a car manufactured by
, 80% would again buy a car manufactured by 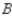 , whereas 10% each would buy cars manufactured by
, whereas 10% each would buy cars manufactured by 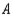 and
and 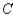 , respectively. Finally, of the customers who bought a car manufactured by
, respectively. Finally, of the customers who bought a car manufactured by 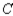 , 75% would again buy a car manufactured by
, 75% would again buy a car manufactured by 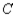 , 5% would buy a car manufactured by
, 5% would buy a car manufactured by 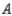 , and 20% would buy a car manufactured by
, and 20% would buy a car manufactured by 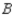 . Assuming that these sentiments reflect the buying habits of customers in the future model years, determine the market share that will be held by each manufacturer in the long run.
. Assuming that these sentiments reflect the buying habits of customers in the future model years, determine the market share that will be held by each manufacturer in the long run.
(Multiple Choice)
4.9/5  (36)
(36)
At the beginning of 1990, the population of a certain state was 53.2% rural and 46.8% urban. Based on past trends, it is expected that 10% of the population currently residing in the rural areas will move into the urban areas, while 16% of the population currently residing in the urban areas will move into the rural areas in the next decade. What was the population distribution in that state at the beginning of 2000?
(Multiple Choice)
4.8/5  (31)
(31)
Determine whether the given two-person, zero-sum matrix game is strictly determined. 
(Multiple Choice)
5.0/5  (33)
(33)
Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie.
Construct the payoff matrix for the game and determine whether the game is strictly determined.
(Multiple Choice)
4.9/5  (38)
(38)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given.
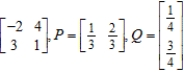
(Essay)
4.7/5  (37)
(37)
Showing 101 - 120 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)