Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first, and identify the submatrices R and S. 
(Multiple Choice)
4.8/5  (39)
(39)
The sum of the entries in each column of a transition matrix must not exceed 1.
(True/False)
4.9/5  (35)
(35)
Roland's Barber Shop and Charley's Barber Shop are both located in the business district of a certain town. Roland estimates that if he raises the price of a haircut by $1, he will increase his market share by 7% if Charley raises his price by the same amount; he will decrease his market share by 2% if Charley holds his price at the same level; and he will decrease his market share by 7% if Charley lowers his price by $1. If Roland keeps his price the same, he will increase his market share by 4% if Charley raises his price by $1; he will keep the same market share if Charley holds the price at the same level; and he will decrease his market share by 4% if Charley lowers his price by $1. Finally, if Roland lowers the price he charges by $1, his market share will increase by 8% if Charley raises his prices by the same amount; he will increase his market share by 4% if Charley holds his price at the same level; and he will increase his market share by 2% if Charley lowers his price by $1.
If neither party is willing to lower the price he charges for a haircut, what strategy should they choose?
(Multiple Choice)
4.8/5  (34)
(34)
Rewrite the absorbing stochastic matrix so that the absorbing states appear first, partition the resulting matrix, and identify the submatrices 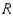 and
and 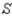 .
. 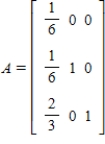
(Multiple Choice)
4.9/5  (34)
(34)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given.
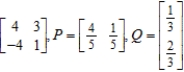
(Essay)
5.0/5  (36)
(36)
Because of the proliferation of more affordable automated office equipment, more and more companies are turning to them as replacements for obsolete equipment. The following transition matrix describes the Markov process. Here, 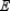 stands for electric typewriters,
stands for electric typewriters, 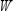 stands for electric typewriters with some form of word processing capabilities, and
stands for electric typewriters with some form of word processing capabilities, and 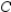 stands for computers with word processing software. E W C
stands for computers with word processing software. E W C 
Rewrite it so that the absorbing state appears first. Partition the resulting matrix and identify the submatrices
Rewrite it so that the absorbing state appears first. Partition the resulting matrix and identify the submatrices 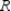 and
and 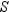 .
.
(Multiple Choice)
4.9/5  (36)
(36)
Determine whether the given matrix is an absorbing stochastic matrix.

(Short Answer)
4.8/5  (37)
(37)
Rewrite the given absorbing stochastic matrix so that the absorbing states appear first and identify the submatrices R and S. 
(Multiple Choice)
4.9/5  (30)
(30)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. 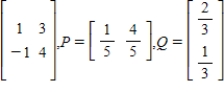
(Multiple Choice)
4.7/5  (42)
(42)
Find 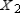 (the probability distribution of the system after two observations) for the given distribution vector
(the probability distribution of the system after two observations) for the given distribution vector 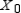 and the given transition matrix
and the given transition matrix 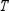 .
. 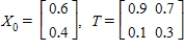
(Multiple Choice)
4.9/5  (40)
(40)
Consider the two-person, zero-sum matrix, strictly determined game.

Find the saddle point(s) of the game.
Find the optimal strategy for each player.
R: row __________ C: column __________
Find the value of the game.
Determine whether the game favors one player over the other.
Find the saddle point(s) of the game.
Find the optimal strategy for each player.
R: row __________ C: column __________
Find the value of the game.
Determine whether the game favors one player over the other.
(Short Answer)
4.7/5  (34)
(34)
Determine whether the matrix is an absorbing stochastic matrix. 
(Multiple Choice)
4.8/5  (37)
(37)
Consider the two-person, zero-sum matrix, strictly determined game. 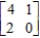
Find the value of the game.
Find the value of the game.
(Multiple Choice)
4.8/5  (32)
(32)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. 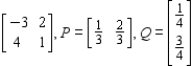
(Multiple Choice)
4.9/5  (37)
(37)
Determine whether the given two-person, zero-sum matrix game is strictly determined.

(Essay)
4.7/5  (30)
(30)
Find the steady-state vector for the transition matrix. 
(Multiple Choice)
4.7/5  (41)
(41)
Determine the maximin and minimax strategies for the two-person, zero-sum matrix game. 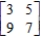
(Multiple Choice)
4.8/5  (34)
(34)
Showing 141 - 160 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)