Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Find the graphical solution of the inequality.
6x - 18 < 0
(Multiple Choice)
4.8/5  (42)
(42)
Determine graphically the solution set for the system of inequalities. 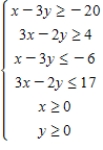
(Multiple Choice)
4.8/5  (33)
(33)
Solve the following linear programming problem by the method of corners. Find the maximum and minimum of 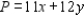 subject to
subject to 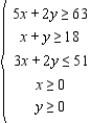
(Multiple Choice)
4.7/5  (35)
(35)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 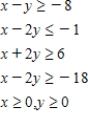
(Multiple Choice)
4.9/5  (32)
(32)
Find the optimal (maximum and minimum) values of the objective function on the feasible set 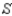 .
. 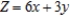
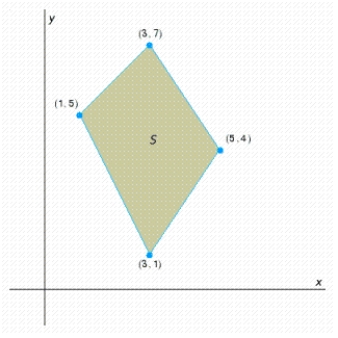
(Multiple Choice)
4.9/5  (33)
(33)
Consider the production problem:  Find the shadow price for resource 2. Identify the binding and nonbinding constraints.
Find the shadow price for resource 2. Identify the binding and nonbinding constraints.
(Multiple Choice)
4.9/5  (35)
(35)
Solve the linear programming problem by the method of corners. Maximize 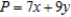 subject to
subject to 
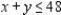
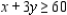
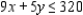
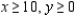
(Multiple Choice)
4.7/5  (30)
(30)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 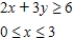
(Multiple Choice)
4.8/5  (45)
(45)
Solve the linear programming problem by the method of corners. Maximize 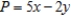 subject to
subject to 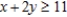
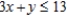
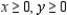
(Multiple Choice)
4.9/5  (35)
(35)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The following problem is a linear programming problem.
Minimize 
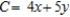 subject to:
subject to: 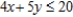 x - y = 0
x - y = 0 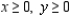

(Multiple Choice)
4.9/5  (41)
(41)
Custom Office Furniture Company is introducing a new line of executive desks made from a specially selected grade of walnut. Initially, three different models-A, B, and C-are to be marketed. Each model A desk requires 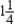 hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model B desk requires
hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model B desk requires 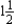 hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model C desk requires
hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model C desk requires 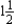 hr,
hr, 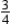 hr, and
hr, and 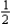 hr for fabrication, assembly, and finishing, respectively. The profit on each model A desk is $26, the profit on each model B desk is $28, and the profit on each model C desk is $24. The total time available in the fabrication department, the assembly department, and the finishing department in the first month of production is 240 hr, 160 hr, and 150 hr, respectively. To maximize Custom's profit, how many desks of each model should be made in the month?
hr for fabrication, assembly, and finishing, respectively. The profit on each model A desk is $26, the profit on each model B desk is $28, and the profit on each model C desk is $24. The total time available in the fabrication department, the assembly department, and the finishing department in the first month of production is 240 hr, 160 hr, and 150 hr, respectively. To maximize Custom's profit, how many desks of each model should be made in the month?
(Multiple Choice)
4.9/5  (33)
(33)
Solve the following linear programming problem by the method of corners.
Maximize 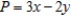
Subject to
Subject to 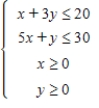
(Multiple Choice)
4.9/5  (32)
(32)
You are given a linear programming problem.Use the method of corners to solve the problem. Minimize 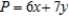
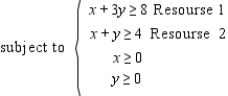
(Multiple Choice)
4.7/5  (36)
(36)
Patricia has at most $36,000 to invest in securities in the form of corporate stocks. She has narrowed her choices to two groups of stocks: growth stocks that she assumes will yield a 11% return (dividends and capital appreciation) within a year and speculative stocks that she assumes will yield a 22% return (mainly in capital appreciation) within a year. Determine how much she should invest in each group of stocks in order to maximize the return on her investments within a year if she has decided to invest at least 3 times as much in growth stocks as in speculative stocks.
(Multiple Choice)
4.9/5  (28)
(28)
Use the method of corners to solve the problem. Find the range of values that the coefficient of x can assume without changing the optimal solution.
Find the range of values that requirement 1 can assume.
Find the shadow price for requirement 1.
Identify the binding and nonbinding constraints. 
(Multiple Choice)
4.9/5  (38)
(38)
Formulate but do not solve the following exercise as a linear programming problem. Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 4 lb of cast iron and 6 min of labor. To produce each model B grate requires 5 lb of cast iron and 3 min of labor. The profit for each model A grate is $2.00, and the profit for each model B grate is $1.50. If 1,100 lb of cast iron and 20 hr of labor are available for the production of grates per day, how many grates of each model should the division produce per day in order to maximize Kane's profits?
(Multiple Choice)
4.8/5  (33)
(33)
Showing 181 - 200 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)