Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Write a system of linear inequalities that describes the shaded region. 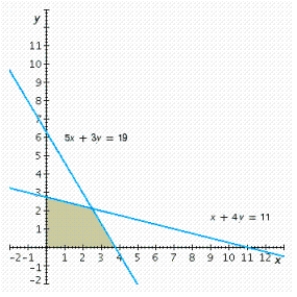
(Multiple Choice)
4.7/5  (27)
(27)
Soundex produces two models of clock radios. Model A requires 15 min of work on assembly line I and 10 min of work on assembly line II. Model B requires 9 min of work on assembly line I and 12 min of work on assembly line II. At most 25 hr of assembly time on line I and 21 hr of assembly time on line II are available each day. Soundex anticipates a profit of $12 on model A and $10 on model B. Because of previous overproduction, management decides to limit the production of model A clock radios to no more than 80/day. The range of values that the contribution to the profit of a model A clock radio can assume without changing the optimal solution is 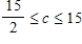 . If the contribution to the profit of a model A clock radio is changed to $9.50/radio, will the original optimal solution still hold? Answer yes or no. __________
What will be the optimal profit? Round to the nearest dollar. $ __________
. If the contribution to the profit of a model A clock radio is changed to $9.50/radio, will the original optimal solution still hold? Answer yes or no. __________
What will be the optimal profit? Round to the nearest dollar. $ __________
(Essay)
4.7/5  (37)
(37)
Consider the production problem: One company wishes to produce two types of souvenirs: type A and type B. Each type-A souvenir will result in a profit of $1, and each type-B souvenir will result in a profit of $1.2. To manufacture a type-A souvenir requires 2 minutes on machine I and 1 minute on machine II. A type-B souvenir requires 1 minute on machine I and 3 minutes on machine II.There are 180 minutes available on machine I and 300 minutes available on machine II for processing the order.
Maximaze 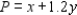 Objective function
Subject to
Objective function
Subject to 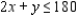 Constrained 1
Constrained 1 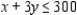 Constrained 2
Constrained 2 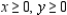 Now suppose the time available on machine I is changed from 180 minutes to (180 + h) minutes, where h is a real number. Then the constraint on machine I is changed to
Now suppose the time available on machine I is changed from 180 minutes to (180 + h) minutes, where h is a real number. Then the constraint on machine I is changed to 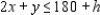 But the line with equation
But the line with equation 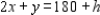 is parallel to the line
is parallel to the line 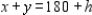 associated with the original constraint 1.
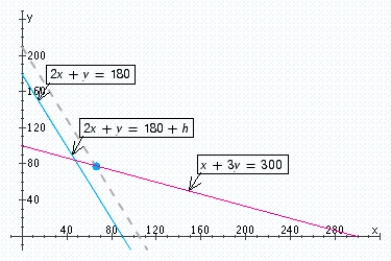
As you can see from the figure , the result of adding the constant h to the right-hand side of constraint 1 is to shift the current optimal solution from the point C to the new optimal solution occurring at the point C. To find the coordinates of C, we observe that C is the point of intersection of the lines with equations
associated with the original constraint 1.
As you can see from the figure , the result of adding the constant h to the right-hand side of constraint 1 is to shift the current optimal solution from the point C to the new optimal solution occurring at the point C. To find the coordinates of C, we observe that C is the point of intersection of the lines with equations  Thus, the coordinates of the point are found by solving the system of linear equations
Thus, the coordinates of the point are found by solving the system of linear equations 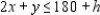
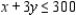
 The solutions are
The solutions are 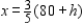 and
and 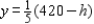 The nonnegativity of x implies that
The nonnegativity of x implies that 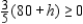
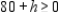
 Next, the nonnegativity of y implies that
Next, the nonnegativity of y implies that 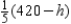

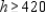 Thus, h must satisfy the inequalities
Thus, h must satisfy the inequalities 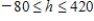 . Computations reveal that for a meaningful solution the time available for machine I must range between (180 - 80) and (180 + 420) minutes-that is, between 100 and 600 minutes.
According to the problem, optimal solution would be
. Computations reveal that for a meaningful solution the time available for machine I must range between (180 - 80) and (180 + 420) minutes-that is, between 100 and 600 minutes.
According to the problem, optimal solution would be 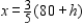 and
and 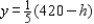 The resulting profit is calculated as follows:
The resulting profit is calculated as follows: 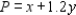
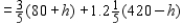
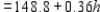 Upon setting h = 1, we find
Upon setting h = 1, we find 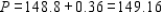 Since the optimal profit for the original problem is $159.6, we see that the shadow price for the first resource is 149.16 - 148.80, or $.36.
Show that if the time available on machine II is changed from 300 min to (300 + k) min, with no change in the maximum capacity for machine I, then company profit is maximized by producing
Since the optimal profit for the original problem is $159.6, we see that the shadow price for the first resource is 149.16 - 148.80, or $.36.
Show that if the time available on machine II is changed from 300 min to (300 + k) min, with no change in the maximum capacity for machine I, then company profit is maximized by producing 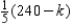 type-A souvenirs and
type-A souvenirs and 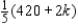 type-B souvenirs, where
type-B souvenirs, where 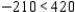 .
.
(Multiple Choice)
4.9/5  (28)
(28)
National Business Machines manufactures two models of fax machines: A and B. Each model A costs $58 to make, and each model B costs $150. The profits are $37 for each model A and $60 for each model B fax machine. The total number of fax machines demanded per month does not exceed 2,700 and the company has earmarked no more than $740,000/month for manufacturing costs.
How many units of each model should National make each month in order to maximize its monthly profits? 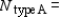 __________
__________ 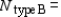 __________
What is the optimal profit?
__________
What is the optimal profit? 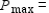 $ __________
$ __________
(Essay)
4.7/5  (35)
(35)
Write a system of linear inequalities that describes the shaded region.
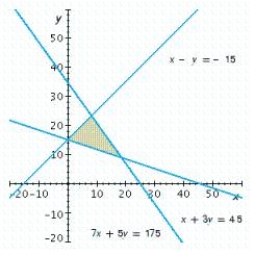
Answer
Answer 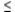 or
or 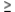 .
.
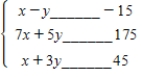
(Essay)
4.7/5  (39)
(39)
You are given a linear programming problem. Use the method of corners to solve the problem.
Maximize 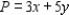

 = __________
= __________ 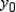 = __________
= __________ 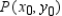 = __________
Find the range of values that the coefficient of x can assume without changing the optimal solution.
≤ c ≤
Find the range of values that resource 1 can assume.
≤ b ≤
Find the shadow price for resource 1. Express your answer to two decimal places, if necessary.
$ __________
Identify the binding and nonbinding constraints.
Constraint 1 is __________
Constraint 2 is __________
Constraint 3 is __________
= __________
Find the range of values that the coefficient of x can assume without changing the optimal solution.
≤ c ≤
Find the range of values that resource 1 can assume.
≤ b ≤
Find the shadow price for resource 1. Express your answer to two decimal places, if necessary.
$ __________
Identify the binding and nonbinding constraints.
Constraint 1 is __________
Constraint 2 is __________
Constraint 3 is __________
(Essay)
4.9/5  (40)
(40)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 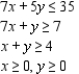
(Multiple Choice)
4.7/5  (34)
(34)
Solve the linear programming problem by the method of corners.  x = __________; y = __________; P = __________
x = __________; y = __________; P = __________
(Essay)
4.9/5  (38)
(38)
Solve the linear programming problem by the method of corners. Maximize 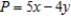 subject to
subject to 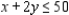
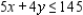
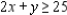
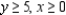
(Multiple Choice)
4.8/5  (29)
(29)
Find the optimal (maximum and minimum) values of the objective function on the feasible set S. If no maximum or minimum value exists, enter no.
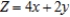
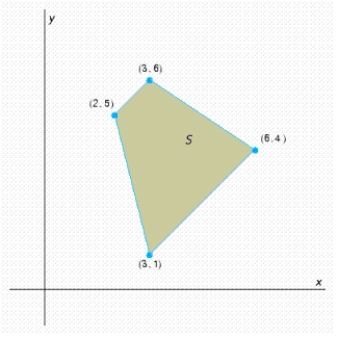
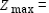 __________,
__________, 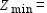 __________
__________
(Essay)
4.8/5  (24)
(24)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 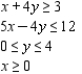
(Multiple Choice)
4.9/5  (33)
(33)
Soundex produces two models of clock radios. Model A requires 15 min of work on assembly line I and 10 min of work on assembly line II. Model B requires 12 min of work on assembly line I and 20 min of work on assembly line II. At most 21 hr of assembly time on line I and 19 hr of assembly time on line II are available each day. Soundex anticipates a profit of $12 on model A and $10 on model B. Because of previous overproduction, management decides to limit the production of model A clock radios to no more than 80/day.
Find the range of values that the resource associated with the time constraint on machine I can assume. Find the shadow price for the resource associated with the time constraint on machine I. Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (40)
(40)
Formulate but do not solve the following exercise as a linear programming problem. A financier plans to invest up to $5 million in three projects. She estimates that project A will yield a return of 11% on her investment, project B will yield a return of 16% on her investment, and project C will yield a return of 23% on her investment. Because of the risks associated with the investments, she decided to put not more than 40% of her total investment in project C. She also decided that her investments in projects B and C should not exceed 70% of her total investment. Finally, she decided that her investment in project A should be at least 70% of her investments in projects B and C. How much should the financier invest in each project if she wishes to maximize the total returns on her investments?
(Multiple Choice)
4.9/5  (26)
(26)
A finance company has a total of $25 million earmarked for homeowner and auto loans. On the average, homeowner loans have a 8% annual rate of return, whereas auto loans yield a 12% annual rate of return. Management has also stipulated that the total amount of homeowner loans should be greater than or equal to 4 times the total amount of automobile loans. Determine the total amount of loans of each type the company should extend to each category in order to maximize its returns.
$ __________ million in homeowner loans, $ __________ million in auto loans
What are the optimal returns? (Round your answer to the nearest hundredth, if necessary).
$ __________ million
(Essay)
4.8/5  (35)
(35)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 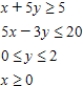
(Multiple Choice)
4.9/5  (33)
(33)
Solve the linear programming problem by the method of corners. 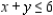 x = __________; y = __________; P = __________
x = __________; y = __________; P = __________
(Essay)
4.9/5  (30)
(30)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 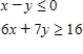
(Multiple Choice)
4.7/5  (34)
(34)
Solve the following linear programming problem by the method of corners. 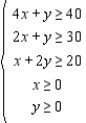
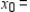 __________
__________ 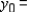 __________
__________ 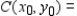 __________
__________
(Short Answer)
4.9/5  (33)
(33)
Showing 161 - 180 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)