Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
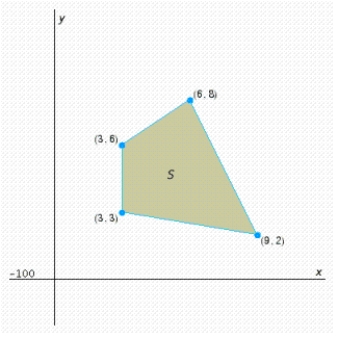
Find the optimal (maximum and minimum) values of the objective function on the feasible set  . If no maximum or minimum value exists, enter no.
. If no maximum or minimum value exists, enter no. 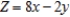
 __________,
__________, 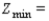 __________
__________
(Essay)
4.9/5  (30)
(30)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 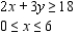
(Multiple Choice)
5.0/5  (33)
(33)
Write a system of linear inequalities that describes the shaded region. 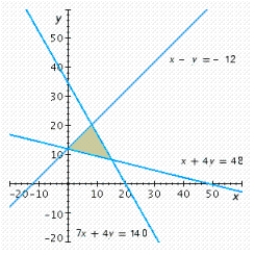
(Multiple Choice)
4.8/5  (25)
(25)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 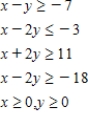
(Multiple Choice)
4.8/5  (33)
(33)
Soundex produces two models of clock radios. Model A requires 15 min of work on assembly line I and 10 min of work on assembly line II. Model B requires 12 min of work on assembly line I and 20 min of work on assembly line II. At most 21 hr of assembly time on line I and 20 hr of assembly time on line II are available each day. Soundex anticipates a profit of $12 on model A and $10 on model B. Because of previous overproduction, management decides to limit the production of model A clock radios to no more than 80/day.
To maximize Soundex's profit, how many clock radios of each model should be produced each day? Find the range of values that the contribution to the profit of a model A clock radio can assume without changing the optimal solution. Identify the binding and nonbinding constraints.
(Multiple Choice)
4.7/5  (39)
(39)
Determine graphically the solution set for the system of inequalities. 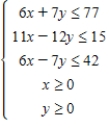
(Multiple Choice)
5.0/5  (33)
(33)
Write a system of linear inequalities that describes the shaded region. 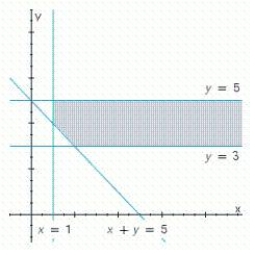
(Multiple Choice)
5.0/5  (35)
(35)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 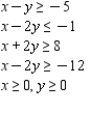
(Multiple Choice)
4.8/5  (37)
(37)
Solve the linear programming problem by the method of corners. Minimize 
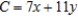 subject to
subject to 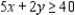
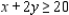
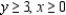
(Multiple Choice)
4.9/5  (35)
(35)
A farmer plans to plant two crops, A and B. The cost of cultivating crop A is $40/acre, whereas that of crop B is $60/acre. The farmer has a maximum of $5,400 available for land cultivation. Each acre of crop A requires 20 labor-hours, and each acre of crop B requires 25 labor-hours. The farmer has a maximum of 2,300 labor-hours available. If she expects to make a profit of $150/acre on crop A and $200/acre on crop B, how many acres of each crop should she plant in order to maximize her profit?
Find the range of values that the contribution to the profit of an acre of crop A can assume without changing the optimal solution.
Find the range of values that the resource associated with the constraint on the land available can assume.
Find the shadow price for the resource associated with the constraint on the land available.
(Multiple Choice)
4.9/5  (35)
(35)
Find the optimal (maximum and/or minimum) value(s) of the given objective function on the feasible set S. Z = x + 6y 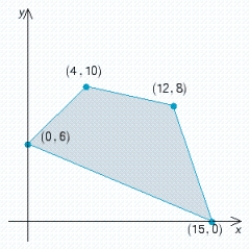
(Multiple Choice)
4.8/5  (35)
(35)
Write a system of linear inequalities that describes the shaded region. 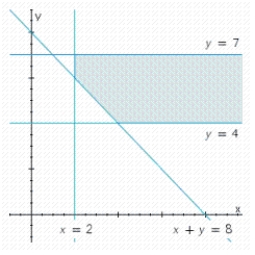
(Multiple Choice)
4.8/5  (44)
(44)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 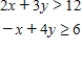
(Multiple Choice)
4.8/5  (35)
(35)
Write a system of linear inequalities that describes the shaded region. 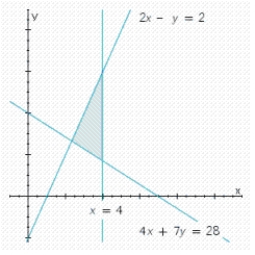
(Multiple Choice)
4.9/5  (31)
(31)
Formulate but do not solve the following exercise as a linear programming problem. TMA manufactures 19-in. color television picture tubes in two separate locations, location I and location II. The output at location I is at most 6,000 tubes/month, whereas the output at location II is at most 5,000/month. TMA is the main supplier of picture tubes to Pulsar Corporation, its holding company, which has priority in having all its requirements met. In a certain month, Pulsar placed orders for 3,000 and 4,000 picture tubes to be shipped to two of its factories located in city A and city B, respectively. The shipping costs (in dollars) per picture tube from the two TMA plants to the two Pulsar factories are as follows:  Find a shipping schedule that meets the requirements of both companies while keeping costs to a minimum.
Find a shipping schedule that meets the requirements of both companies while keeping costs to a minimum.
(Multiple Choice)
4.9/5  (29)
(29)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 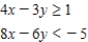
(Multiple Choice)
4.9/5  (36)
(36)
Solve the linear programming problem by the method of corners. Minimize 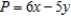 subject to
subject to 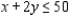
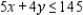
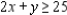
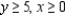
(Multiple Choice)
4.9/5  (33)
(33)
Determine graphically the solution set for the following system of inequalities. 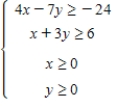
(Multiple Choice)
4.8/5  (30)
(30)
A division of the Winston Furniture Company manufactures dining tables and chairs. Each table requires 40 board feet of wood and 3 labor-hours. Each chair requires 16 board feet of wood and 4 labor-hours. The profit for each table is 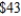 , and the profit for each chair is
, and the profit for each chair is 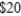 . In a certain week, the company has
. In a certain week, the company has 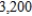 board feet of wood available and
board feet of wood available and 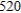 labor-hours available. How many tables and chairs should Winston manufactures to maximize its profit? What is the maximum profit?
labor-hours available. How many tables and chairs should Winston manufactures to maximize its profit? What is the maximum profit?
(Multiple Choice)
4.7/5  (32)
(32)
Showing 81 - 100 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)