Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
A hunger-relief organization has earmarked between $2 and $2.5 million, inclusive, for aid to two African countries, country A and country B. Country A is to receive between $1 and $1.5 million, inclusive, in aid, and country B is to receive at least $0.75 million in aid. It has been estimated that each dollar spent in country A will yield an effective return of $.75, whereas a dollar spent in country B will yield an effective return of $.85. How should the aid be allocated if the money is to be utilized most effectively according to these criteria? (Hint: If x and y denote the amount of money to be given to country A and country B, respectively, then the objective function to be maximized is P = 0.75x + 0.85y.)
(Multiple Choice)
4.7/5  (26)
(26)
National Business Machines manufactures two models of fax machines: A and B. Each model A costs $125 to make, and each model B costs $150. The profits are $32 for each model A and $43 for each model B fax machine. The total number of fax machines demanded per month does not exceed 2,600 and the company has earmarked no more than $550,000/month for manufacturing costs. How many units of each model should National make each month in order to maximize its monthly profits? What is the optimal profit?
(Multiple Choice)
4.9/5  (41)
(41)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 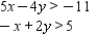
(Multiple Choice)
4.8/5  (42)
(42)
Solve the linear programming problem by the method of corners. Maximize 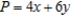 subject to
subject to 
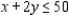
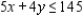
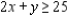
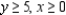
(Multiple Choice)
4.9/5  (40)
(40)
Write a system of linear inequalities that describes the shaded region. 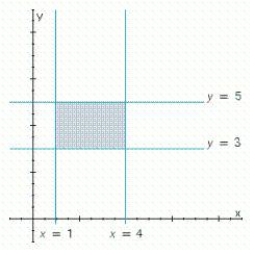
(Multiple Choice)
4.9/5  (39)
(39)
Write a system of linear inequalities that describes the shaded region. 
(Multiple Choice)
4.9/5  (44)
(44)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
The following problem is a linear programming problem.
Minimize 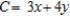 subject to:
subject to: 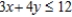 x - y = 0
x ≥ 0, y ≥ 0
x - y = 0
x ≥ 0, y ≥ 0
(True/False)
4.9/5  (30)
(30)
Find the optimal (maximum and/or minimum) value(s) of the given objective function on the feasible set S. If no maximum or minimum value exists, enter no.
Z = 5x + 8y 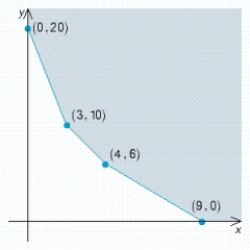 Max.: __________, min.: __________
Max.: __________, min.: __________
(Essay)
4.8/5  (35)
(35)
Deluxe River Cruises operates a fleet of river vessels. The fleet has two types of vessels: a type-A vessel has 60 deluxe cabins and 160 standard cabins, whereas a type-B vessel has 80 deluxe cabins and 120 standard cabins. Under a charter agreement with the Odyssey Travel Agency, Deluxe River Cruises is to provide Odyssey with a minimum of 620 deluxe and 1,280 standard cabins for their 16-day cruise in May. It costs $65,000 to operate a type-A vessel and $54,000 to operate a type-B vessel for that period. Find the range of values that the requirement for deluxe cabins can assume.
(Multiple Choice)
4.9/5  (40)
(40)
Solve the linear programming problem by the method of corners.  x = __________; y = __________; C = __________
x = __________; y = __________; C = __________
(Essay)
4.9/5  (32)
(32)
Write a system of linear inequalities that describes the shaded region. 
(Multiple Choice)
4.8/5  (36)
(36)
Use the method of corners to solve the problem. Find the range of values that the coefficient of x can assume without changing the optimal solution.
Find the range of values that requirement 1 can assume.
Find the shadow price for requirement 1.
Identify the binding and nonbinding constraints. 
(Multiple Choice)
4.7/5  (34)
(34)
Showing 201 - 214 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)