Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
You are given a linear programming problem. Use the method of corners to solve the problem.
Maximize P = 6x + 4y 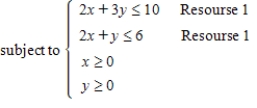 x0 = __________
y0 = __________
P(x0, y0) = __________
Find the range of values that the coefficient of x can assume without changing the optimal solution.
≤ c ≤
Find the range of values that resource 1 can assume.
≤ b ≤
Find the shadow price for resource 1. Enter your answer to two decimal places.
$ __________
Identify the binding and nonbinding constraints.
Constraint 1 is __________
Constraint 2 is __________
x0 = __________
y0 = __________
P(x0, y0) = __________
Find the range of values that the coefficient of x can assume without changing the optimal solution.
≤ c ≤
Find the range of values that resource 1 can assume.
≤ b ≤
Find the shadow price for resource 1. Enter your answer to two decimal places.
$ __________
Identify the binding and nonbinding constraints.
Constraint 1 is __________
Constraint 2 is __________
(Essay)
5.0/5  (30)
(30)
Write a system of linear inequalities that describes the shaded region.
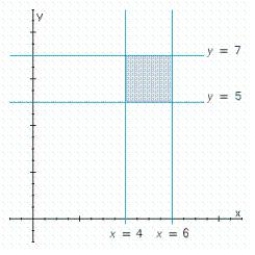
(Essay)
4.9/5  (28)
(28)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 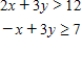
(Multiple Choice)
4.7/5  (35)
(35)
You are given a linear programming problem. Use the method of corners to solve the problem.
Minimize 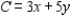
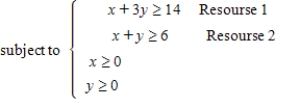
 = __________
= __________ 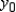 = __________
= __________ 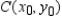 = __________
Find the range of values that the coefficient of
= __________
Find the range of values that the coefficient of 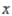 can assume without changing the optimal solution.
≤ c ≤
Find the range of values that requirement 1 can assume.
≤ b ≤
Find the shadow price for requirement 1. Enter your answer to two decimal places, if necessary.
$ __________
Identify the binding and nonbinding constraints.
Constraint 1 is __________
Constraint 2 is __________
can assume without changing the optimal solution.
≤ c ≤
Find the range of values that requirement 1 can assume.
≤ b ≤
Find the shadow price for requirement 1. Enter your answer to two decimal places, if necessary.
$ __________
Identify the binding and nonbinding constraints.
Constraint 1 is __________
Constraint 2 is __________
(Essay)
4.9/5  (27)
(27)
Formulate but do not solve the following exercise as a linear programming problem. Perth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $15,000/day to operate, and it yields 30 oz of gold and 3,000 oz of silver each day. The Horseshoe Mine costs $17,000/day to operate, and it yields 65 oz of gold and 1,000 oz of silver each day. Company management has set a target of at least 550 oz of gold and 17,000 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost?
(Multiple Choice)
4.7/5  (34)
(34)
Solve the linear programming problem by the method of corners. 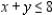 x = __________; y = __________; P = __________
x = __________; y = __________; P = __________
(Essay)
4.9/5  (31)
(31)
A veterinarian has been asked to prepare a diet for a group of dogs to be used in a nutrition study at the School of Animal Science. It has been stipulated that each serving should be no larger than 8 oz and must contain at least 29 units of nutrient I and 20 units of nutrient II. The vet has decided that the diet may be prepared from two brands of dog food: brand A and brand B. Each ounce of brand A contains 3 units of nutrient I and 4 units of nutrient II. Each ounce of brand B contains 5 units of nutrient I and 2 units of nutrient II. Brand A costs 5 cents/ounce and brand B costs 9 cents/ounce. Determine how many ounces of each brand of dog food should be used per serving to meet the given requirements at a minimum cost.
(Multiple Choice)
4.9/5  (28)
(28)
Formulate but do not solve the following exercise as a linear programming problem. Deluxe River Cruises operates a fleet of river vessels. The fleet has two types of vessels: A type-A vessel has 70 deluxe cabins and 150 standard cabins, whereas a type-B vessel has 80 deluxe cabins and 110 standard cabins. Under a charter agreement with Odyssey Travel Agency, Deluxe River Cruises is to provide Odyssey with a minimum of 390 deluxe and 690 standard cabins for their 15-day cruise in May. It costs $43,000 to operate a type-A vessel and $52,000 to operate a type-B vessel for that period. How many of each type vessel should be used in order to keep the operating costs to a minimum?
(Multiple Choice)
4.8/5  (41)
(41)
Soundex produces two models of clock radios. Model A requires 15 min of work on assembly line I and 10 min of work on assembly line II. Model B requires 12 min of work on assembly line I and 20 min of work on assembly line II. At most 21 hr of assembly time on line I and 22 hr of assembly time on line II are available each day. Soundex anticipates a profit of $12 on model A and $10 on model B. Because of previous overproduction, management decides to limit the production of model A clock radios to no more than 90/day. The range of values that the contribution to the profit of a model A clock radio can assume without changing the optimal solution is 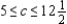 . If the contribution to the profit of a model A clock radio is changed to $6.50/radio, will the original optimal solution still hold? What will be the optimal profit?
. If the contribution to the profit of a model A clock radio is changed to $6.50/radio, will the original optimal solution still hold? What will be the optimal profit?
(Multiple Choice)
4.9/5  (33)
(33)
Perth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $16,000/day to operate, and it yields 50 oz of gold and 3,000 oz of silver per day. The Horseshoe Mine costs $17,000/day to operate, and it yields 75 oz of gold and 1,000 ounces of silver each day. Company management has set a target of at least 825 oz of gold and 18,000 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost? Find the range of values that the cost of operating the Saddle Mine per day can assume without changing the optimal solution.
Find the range of values that the requirement for gold can assume.
Find the shadow price for the requirement for gold.
(Multiple Choice)
4.8/5  (31)
(31)
Determine graphically the solution set for the system of inequalities. 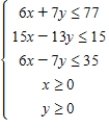
(Multiple Choice)
4.9/5  (40)
(40)
Use the method of corners to solve the problem. Find the range of values that the coefficient of x can assume without changing the optimal solution.
Find the range of values that resource 1 can assume.
Find the shadow price for resource 1.
Identify the binding and nonbinding constraints. 
(Multiple Choice)
4.8/5  (28)
(28)
Write a system of linear inequalities that describes the shaded region. 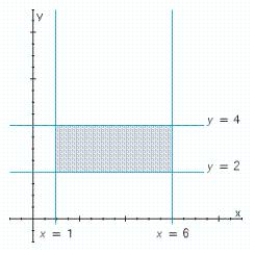
(Multiple Choice)
4.7/5  (33)
(33)
A farmer plans to plant two crops, A and B. The cost of cultivating crop A is $40/acre, whereas that of crop B is $60/acre. The farmer has a maximum of $7,400 available for land cultivation. Each acre of crop A requires 20 labor-hours, and each acre of crop B requires 25 labor-hours. The farmer has a maximum of 3,300 labor-hours available. If he expects to make a profit of $220/acre on crop A and $280/acre on crop B, how many acres of each crop should he plant in order to maximize his profit?
(Multiple Choice)
4.9/5  (34)
(34)
Determine graphically the solution set for the following system of inequalities. 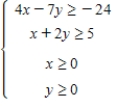
(Multiple Choice)
4.9/5  (36)
(36)
Write a system of linear inequalities that describes the shaded region. 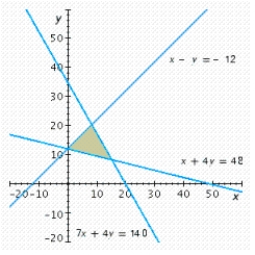 Answer
Answer 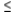 or
or 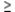 .
. 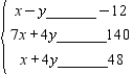
(Essay)
4.8/5  (36)
(36)
Find the optimal (maximum and/or minimum) value(s) of the given objective function on the feasible set S. If no maximum or minimum value exists, enter no.
Z = x + 9y 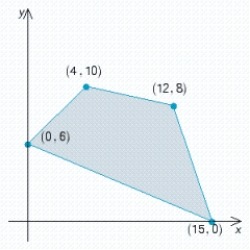 Max.: __________, min.: __________
Max.: __________, min.: __________
(Essay)
4.8/5  (37)
(37)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 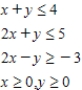
(Multiple Choice)
4.9/5  (28)
(28)
Solve the linear programming problem by the method of corners. Maximize 
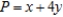 subject to
subject to 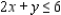
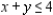
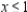
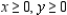
(Multiple Choice)
4.7/5  (31)
(31)
Showing 141 - 160 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)