Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Find the graphical solution of the inequality.
5x - 10 < 0
(Multiple Choice)
4.8/5  (37)
(37)
Write a system of linear inequalities that describes the shaded region.
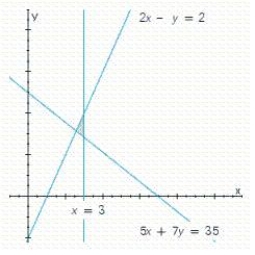
(Essay)
4.8/5  (29)
(29)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 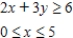
(Multiple Choice)
4.7/5  (38)
(38)
Write a system of linear inequalities that describes the shaded region. 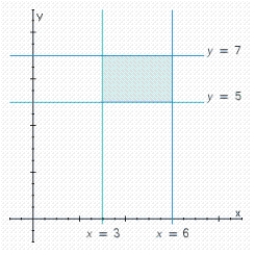
(Essay)
4.9/5  (36)
(36)
Determine graphically the solution set for the following system of inequalities. 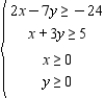
(Multiple Choice)
4.8/5  (33)
(33)
Formulate but do not solve the following exercise as a linear programming problem. A nutritionist at the Medical Center has been asked to prepare a special diet for certain patients. He has decided that the meals should contain a minimum of 400 mg of calcium, 9 mg of iron, and 35 mg of vitamin C. He has further decided that the meals are to be prepared from foods A and B. Each ounce of food A contains 35 mg of calcium, 1 mg of iron, 3 mg of vitamin C, and 3 mg of cholesterol. Each ounce of food B contains 25 mg of calcium, 0.6 mg of iron, 7 mg of vitamin C, and 7 mg of cholesterol. Find how many ounces of each type of food should be used in a meal so that the cholesterol content is minimized and the minimum requirements of calcium, iron, and vitamin C are met.
(Multiple Choice)
4.9/5  (35)
(35)
Solve the linear programming problem by the method of corners. Minimize 
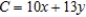 subject to
subject to 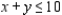
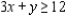
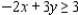
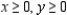
(Multiple Choice)
4.8/5  (38)
(38)
D11etermine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 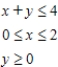
(Multiple Choice)
4.9/5  (41)
(41)
Write a system of linear inequalities that describes the shaded region. 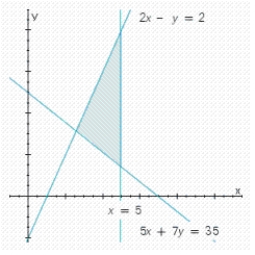
(Essay)
4.8/5  (26)
(26)
A farmer plans to plant two crops, A and B. The cost of cultivating crop A is $40/acre, whereas that of crop B is $60/acre. The farmer has a maximum of $7,400 available for land cultivation. Each acre of crop A requires 20 labor-hours, and each acre of crop B requires 25 labor-hours. The farmer has a maximum of 3,300 labor-hours available. If he expects to make a profit of $100/acre on crop A and $140/acre on crop B, how many acres of each crop should he plant in order to maximize his profit?
__________ acres of crop A, __________ acres of crop B
What is the optimal profit? $ __________
(Essay)
4.7/5  (32)
(32)
Solve the linear programming problem by the method of corners.
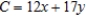 x = __________; y = __________; C = __________
x = __________; y = __________; C = __________
(Essay)
4.8/5  (37)
(37)
Write a system of linear inequalities that describes the shaded region.
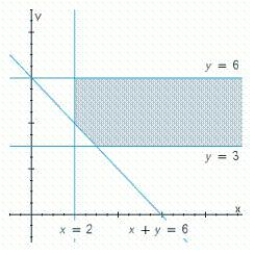
(Essay)
4.9/5  (33)
(33)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 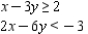
(Multiple Choice)
4.8/5  (29)
(29)
Determine graphically the solution set for the system of inequalities. 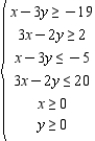
(Multiple Choice)
4.9/5  (35)
(35)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 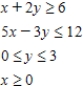
(Multiple Choice)
4.9/5  (30)
(30)
Patricia has at most $36,000 to invest in securities in the form of corporate stocks. She has narrowed her choices to two groups of stocks: growth stocks that she assumes will yield a 13% return (dividends and capital appreciation) within a year and speculative stocks that she assumes will yield a 26% return (mainly in capital appreciation) within a year. Determine how much she should invest in each group of stocks in order to maximize the return on her investments within a year if she has decided to invest at least 3 times as much in growth stocks as in speculative stocks.
$__________ in growth stocks and $ __________ in speculative stocks
maximum return: $ __________
(Essay)
4.8/5  (40)
(40)
You are given a linear programming problem. Find the shadow price for resource 1. Maximize P = 5x + 4y 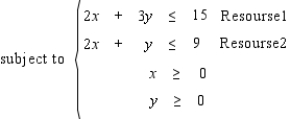
(Multiple Choice)
4.8/5  (36)
(36)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 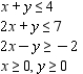
(Multiple Choice)
4.9/5  (34)
(34)
Showing 41 - 60 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)