Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 3 lb of cast iron and 6 min of labor. To produce each model B grate requires 6 lb of cast iron and 3 min of labor. The profit for each model A grate is $2, and the profit for each model B grate is $1.50. 1,170 lb of cast iron and 21 labor-hours are available for the production of grates each day. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 210 grates per day. How many grates of each model should the division produce daily to maximize Kane's profits?
Find the range of values that the resource for cast iron can assume without changing the optimal solution. Find the shadow price for the resource for cast iron. Round your answer to the nearest cent.
(Multiple Choice)
4.7/5  (30)
(30)
AntiFam, a hunger-relief organization, has earmarked between $4 and $4.5 million, inclusive, for aid to two African countries, country A and country B. Country A is to receive between $3 and $3.5 million, inclusive, in aid, and country B is to receive at least $0.75 million in aid. It has been estimated that each dollar spent in country A will yield an effective return of $0.60, whereas a dollar spent in country B will yield an effective return of $0.70. How should the aid be allocated if the money is to be utilized most effectively according to these criteria? Hint: If 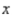 and
and 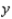 denote the amount of money (in million of dollars) to be given to country A and country B, respectively, then the objective function to be maximized is
denote the amount of money (in million of dollars) to be given to country A and country B, respectively, then the objective function to be maximized is 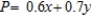 .
.
(Multiple Choice)
4.9/5  (35)
(35)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 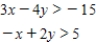
(Multiple Choice)
4.8/5  (31)
(31)
A corporation has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 3 lb of cast iron and 6 min of labor. To produce each model B grate requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is $2.50, and the profit for each model B grate is $1.50. If 1,000 lb of cast iron and 20 labor-hours are available for the production of fireplace grates per day, how many grates of each model should the division produce in order to help maximize the division's profits?
(Multiple Choice)
4.9/5  (38)
(38)
Write a system of linear inequalities that describes the shaded region. 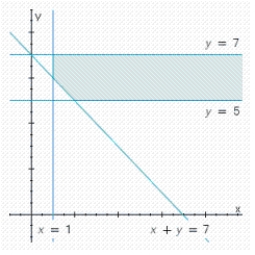
(Essay)
4.8/5  (30)
(30)
Write a system of linear inequalities that describes the shaded region.
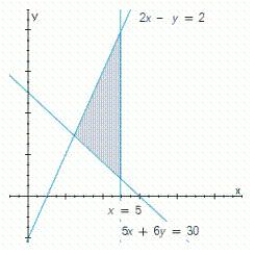
(Essay)
4.8/5  (35)
(35)
Ace Novelty manufactures Gaint Pandas and Saint Bemards. Each Panda requires 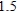 yd2 of plush,
yd2 of plush, 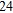 ft3 of stuffing, and
ft3 of stuffing, and  pieces of trim; each Saint Bernard requires
pieces of trim; each Saint Bernard requires  yd2of plush,
yd2of plush,  ft3 of stuffing,
ft3 of stuffing,  pieces of trim. The profit for each Panda is
pieces of trim. The profit for each Panda is  and profit for each Saint Bernard
and profit for each Saint Bernard  . If
. If 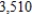 yd2 of plush,
yd2 of plush, 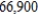 ft3 of stuffing and
ft3 of stuffing and 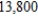 pieces of trim are available, how many of each of the stuffed animals should the company manufacture to maximize the profit?
pieces of trim are available, how many of each of the stuffed animals should the company manufacture to maximize the profit?
(Multiple Choice)
4.9/5  (41)
(41)
Write a system of linear inequalities that describes the shaded region. 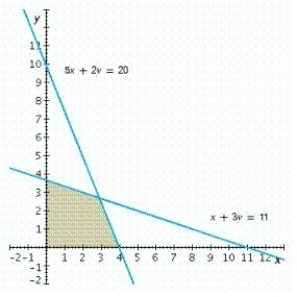 Answer
Answer 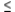 or
or 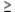 .
. 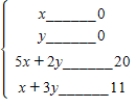
(Essay)
4.7/5  (39)
(39)
You are given a linear programming problem. Find the shadow price for requirement 1. Maximize 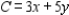

(Multiple Choice)
4.8/5  (32)
(32)
Write a system of linear inequalities that describes the shaded region.
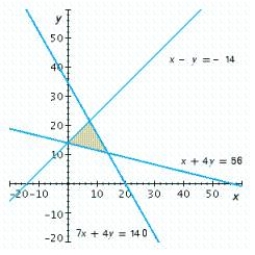
Answer
Answer  or
or  .
.
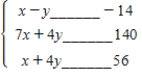
(Essay)
4.9/5  (37)
(37)
A corporation has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 3 lb of cast iron and 6 min of labor. To produce each model B grate requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is $3.00, and the profit for each model B grate is $2.50. If 1,000 lb of cast iron and 20 labor-hours are available for the production of fireplace grates per day, how many grates of each model should the division produce in order to help maximize the division's profits?
__________ model A, __________ model B
What is the optimal profit?
$__________
(Essay)
4.8/5  (35)
(35)
Ashley has earmarked at most $270,000 for investment in three mutual funds: a money market fund, an international equity fund, and a growth-and-income fund. The money market fund has a rate of return of 6% per year, the international equity fund has a rate of return of 10% per year, and the growth-and-income fund has a rate of return of 16% per year. Ashley has stipulated that no more than 25% of her total portfolio should be in the growth-and-income fund and that no more than 50% of her total portfolio should be in the international equity fund. To maximize the return on her investment, how much should Ashley invest in each type of fund?
(Multiple Choice)
4.9/5  (26)
(26)
Write a system of linear inequalities that describes the shaded region.
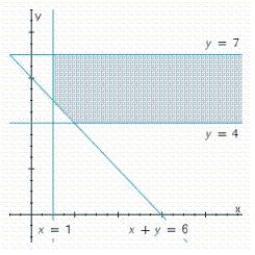
(Essay)
4.9/5  (34)
(34)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 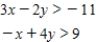
(Multiple Choice)
4.9/5  (26)
(26)
Find the optimal (maximum and/or minimum) value(s) of the given objective function on the feasible set S. If no maximum or minimum value exists, enter no.
Z = 8x + 6y 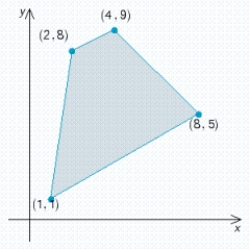 Max.: __________, min.: __________
Max.: __________, min.: __________
(Essay)
4.8/5  (34)
(34)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 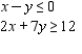
(Multiple Choice)
4.9/5  (36)
(36)
You are given a linear programming problem.Use the method of corners to solve the problem. Maximize 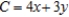
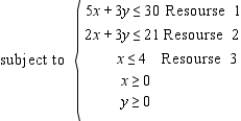
(Multiple Choice)
4.8/5  (28)
(28)
Showing 121 - 140 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)