Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
A division of the Winston Furniture Company manufactures dining tabels and chairs. Each table requires  board feet of wood and
board feet of wood and  labour-hours. Each chair requires
labour-hours. Each chair requires  board feet of wood and
board feet of wood and  labour-hours. The profit for each table is
labour-hours. The profit for each table is 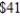 , and the profit for each chair is
, and the profit for each chair is 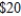 . In a certain week, the company has
. In a certain week, the company has 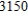 board feet of wood available and
board feet of wood available and 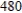 labour-hours. How many tabels and chaires should Winston manufacture to maximize its profits?
labour-hours. How many tabels and chaires should Winston manufacture to maximize its profits?
(Multiple Choice)
4.7/5  (25)
(25)
Formulate but do not solve the following exercise as a linear programming problem.
Everest Deluxe World Travel has decided to advertise in the Sunday editions of two major newspapers in town. These advertisements are directed at three groups of potential customers. Each advertisement in newspaper I is seen by 80,000 group A customers, 30,000 group B customers, and 20,000 group C customers. Each advertisement in newspaper II is seen by 10,000 group A, 30,000 group B, and 60,000 group C customers. Each advertisement in newspaper I costs $1,300, and each advertisement in newspaper II costs $700. Everest would like their advertisements to be read by at least 5,000,000 million people from group A, 1,400,000 million people from group B, and 1 million people from group C. How many advertisements should Everest place in each newspaper to achieve its advertisement goals at a minimum cost?
(Multiple Choice)
4.9/5  (35)
(35)
Formulate but do not solve the following exercise as a linear programming problem. Madison Finance has a total of $15 million earmarked for homeowner and auto loans. On the average, homeowner loans have a 10% annual rate of return, whereas auto loans yield a 11% annual rate of return. Management has also stipulated that the total amount in dollars of homeowner loans should be greater than or equal to nine times the total amount in dollars of automobile loans. Determine the total amount of loans of each type Madison should extend to each category in order to maximize its returns.
(Multiple Choice)
4.8/5  (34)
(34)
Formulate but do not solve the following exercise as a linear programming problem. Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 4 lb of cast iron and 5 min of labor. To produce each model B grate requires 5 lb of cast iron and 4 min of labor. The profit for each model A grate is $4.00, and the profit for each model B grate is $1.50. If 1,000 lb of cast iron and 25 hr of labor are available for the production of grates per day, how many grates of each model should the division produce per day in order to maximize Kane's profits?
Because of a backlog of orders on model A grates, the manager of Kane Manufacturing has decided to produce at least 150 of these models a day. Operating under this additional constraint, how many grates of each model should Kane produce to maximize profit?
(Multiple Choice)
4.7/5  (39)
(39)
Find the optimal (maximum and minimum) values of the objective function on the feasible set 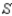 .
. 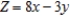
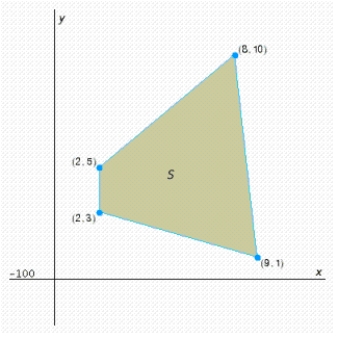
(Multiple Choice)
4.7/5  (27)
(27)
A hunger-relief organization, has earmarked between $2 and $2.5 million, inclusive, for aid to two African countries, country A and country B. Country A is to receive between $1 and $1.5 million, inclusive, in aid, and country B is to receive at least $0.75 million in aid. It has been estimated that each dollar spent in country A will yield an effective return of $.60, whereas a dollar spent in country B will yield an effective return of $.50. How should the aid be allocated if the money is to be utilized most effectively according to these criteria? (Hint: If x and y denote the amount of money to be given to country A and country B, respectively, then the objective function to be maximized is P = 0.6x + 0.5y.)
$ __________ million to country A and $ __________ million to country B
(Essay)
4.8/5  (34)
(34)
Perth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $14,000/day to operate, and it yields 50 oz of gold and 3,000 oz of silver each day. The Horseshoe Mine costs $16,000/day to operate, and it yields 75 oz of gold and 1,000 oz of silver each day. Company management has set a target of at least 650 oz of gold and 11,000 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost?
(Multiple Choice)
4.7/5  (38)
(38)
Determine graphically the solution set for the system of inequalities. 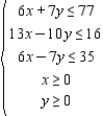
(Multiple Choice)
4.9/5  (25)
(25)
Write a system of linear inequalities that describes the shaded region. 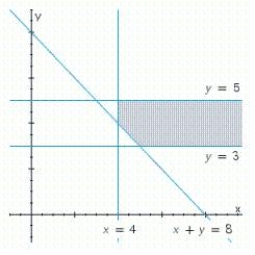
(Multiple Choice)
4.8/5  (34)
(34)
Find the optimal (maximum and/or minimum) value(s) of the given objective function on the feasible set S. Z = 4x + 7y 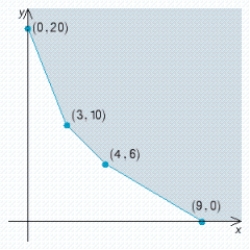
(Multiple Choice)
4.8/5  (30)
(30)
Kane Manufacturing has a division that produces two models of grates, model A and model B. To produce each model A grate requires 3 pounds of cast iron and 6 minutes of labor. To produce each model B grate requires 4 pounds of cast iron and 3 minutes of labor. The profit for each model A grate is $2.00, and the profit for each model B grate is $1.50. Available for grate production each day are 1,160 pounds of cast iron and 22 labor-hours. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 180 grates per day.
Let x denote the number of model A grates and y the number of model B grates produced. Then, the problem can be reduced to a linear programming problem with the objective function P = 2x + 1.5y and constraints
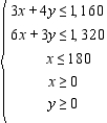
Find the range of values that resource 2 (the constant on the right-hand side of constraint 2) can assume.
≤ C resourse2 ≤
By how much can the right-hand side of constraint 3 be decreased so that the current optimal solution still holds?
It cannot be decreased by more than __________ units.
Find the range of values that resource 2 (the constant on the right-hand side of constraint 2) can assume.
≤ C resourse2 ≤
By how much can the right-hand side of constraint 3 be decreased so that the current optimal solution still holds?
It cannot be decreased by more than __________ units.
(Short Answer)
4.8/5  (36)
(36)
Write a system of linear inequalities that describes the shaded region. 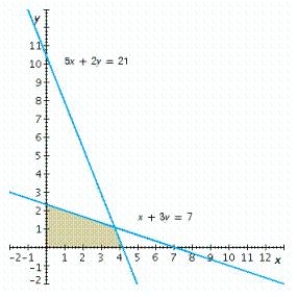
(Multiple Choice)
4.9/5  (38)
(38)
Write a system of linear inequalities that describes the shaded region. 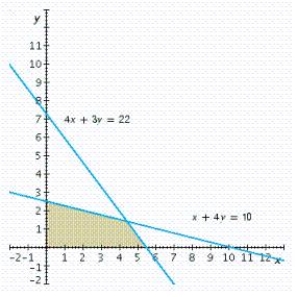
(Multiple Choice)
4.9/5  (24)
(24)
Determine graphically the solution set for the system of inequalities. 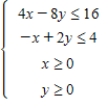
(Multiple Choice)
4.8/5  (33)
(33)
Kane Manufacturing has a division that produces two models of grates, model A and model B. To produce each model A grate requires 3 pounds of cast iron and 6 minutes of labor. To produce each model B grate requires 4 pounds of cast iron and 3 minutes of labor. The profit for each model A grate is $2.00, and the profit for each model B grate is $1.50. Available for grate production each day are 1,560 pounds of cast iron and 22 labor-hours. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 180 grates per day.
Let x denote the number of model A grates and y the number of model B grates produced. Then, the problem can be reduced to a linear programming problem with the objective function P = 2x + 1.5y and constraints

Find the range of values that resource 2 (the constant on the right-hand side of constraint 2) can assume.
Find the range of values that resource 2 (the constant on the right-hand side of constraint 2) can assume.
(Multiple Choice)
4.8/5  (36)
(36)
Ace Novelty wishes to produce two types of souvenirs: type A and type B. Each type-A souvenir will result in a profit of $1.00, and each type-B souvenir will result in a profit of $1.20. To manufacture a type-A souvenir requires 2 minutes on machine I and 1 minute on machine II. A type-B souvenir requires 1 minute on machine I and 3 minutes on machine II. There are 3 hours available on machine I and 5 hours available on machine II for processing the order.
Let x be the number of type-A souvenirs and y be the number of type-B souvenirs to be made. Then the problem can be reduced to a linear programming problem with the objective function P = x + 1.2y and constraints
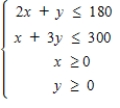
Please enter your answers to two decimal places.
Find the contribution to the profit of a type-B souvenir for which the optimal solution holds.
$ ≤ c type-B ≤ $
What will be the optimal profit of the company if the contribution to the profit of a type-A souvenir is $1.90 (with the contribution to the profit of a type-B souvenir held at $1.20)?
$ __________
What will be the optimal profit of the company if the contribution to the profit of a type-B souvenir is $2.80 (with the contribution to the profit of a type-A souvenir held at $1.00)?
$ __________
Please enter your answers to two decimal places.
Find the contribution to the profit of a type-B souvenir for which the optimal solution holds.
$ ≤ c type-B ≤ $
What will be the optimal profit of the company if the contribution to the profit of a type-A souvenir is $1.90 (with the contribution to the profit of a type-B souvenir held at $1.20)?
$ __________
What will be the optimal profit of the company if the contribution to the profit of a type-B souvenir is $2.80 (with the contribution to the profit of a type-A souvenir held at $1.00)?
$ __________
(Short Answer)
4.8/5  (20)
(20)
Determine graphically the solution set for the system of inequalities. 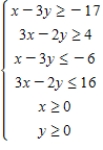
(Multiple Choice)
4.8/5  (38)
(38)
Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 3 lb of cast iron and 6 min of labor. To produce each model B grate requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is $2, and the profit for each model B grate is $1.50. 1,000 lb of cast iron and 23 labor-hours are available for the production of grates each day. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 200 grates per day. How many grates of each model should the division produce daily to maximize Kane's profits? The range of values that the coefficient of x can assume without changing the optimal solution is 1.125 ≤ c ≤ 3.
If the contribution to the profit of a model A grate is changed to $2.05/grate, will the original optimal solution still hold? Answer yes or no. __________
What will be the new optimal solution?
Model A: __________
Model B: __________
Please enter your answer as a dollar value to the nearest cent:
maximum profit: $ __________
(Short Answer)
4.8/5  (39)
(39)
Showing 21 - 40 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)