Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Determine graphically the solution set for the system of inequalities. 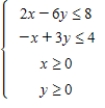
(Multiple Choice)
4.7/5  (31)
(31)
Bayer Pharmaceutical produces three kinds of cold formulas: formula I, formula II, and formula III. It takes 2.5 hr to produce 1,000 bottles of formula I, 3 hr to produce 1,000 bottles of formula II, and 4 hr to produce 1,000 bottles of formula III. The profits for each 1,000 bottles of formula I, formula II, and formula III are $180, $200, and $300, respectively. For a certain production run, there are enough ingredients on hand to make at most 8,000 bottles of formula I, 15,000 bottles of formula II, and 7,000 bottles of formula III. Furthermore, the time for the production run is limited to a maximum of 65 hr. How many bottles of each formula should be produced in this production run so that the profit is maximized?
(Multiple Choice)
4.8/5  (40)
(40)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 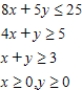
(Multiple Choice)
4.7/5  (29)
(29)
Formulate but do not solve the following exercise as a linear programming problem. A company manufactures two products, A and B, on two machines I and II. It has been determined that the company will realize a profit of $4 on each unit of product A and a profit of $3 on each unit of product B. To manufacture a unit of product A requires 5 min on machine I and 5 min on machine II. To manufacture a unit of product B requires 7 min on machine I and 4 min on machine II. There are 6 hr of machine time available on machine I and 3 hr of machine time available on machine II in each work shift. How many units of each product should be produced in each shift to maximize the company's profit?
(Multiple Choice)
4.9/5  (39)
(39)
Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 3 lb of cast iron and 6 min of labor. To produce each model B grade requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is 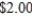 , and the profit for each model B grate is
, and the profit for each model B grate is 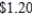 . If
. If 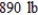 of cast iron and
of cast iron and  labor-hours are available for the production of fireplace grates of each model should the division produce to maximize kane's profit? what is the optimal profit?
labor-hours are available for the production of fireplace grates of each model should the division produce to maximize kane's profit? what is the optimal profit?
(Multiple Choice)
4.9/5  (43)
(43)
Write a system of linear inequalities that describes the shaded region. 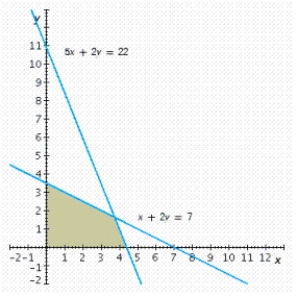 Answer
Answer  or
or 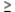 .
. 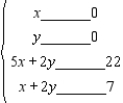
(Essay)
4.9/5  (29)
(29)
National Business Machines manufactures two models of fax machines: A and B. Each model A cost 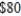 to make, and each model B cost
to make, and each model B cost 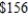 .The profits are
.The profits are 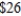 for each model A and
for each model A and 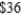 for each model B fax machine. If the total number of fax machines demanded per month does not exceed
for each model B fax machine. If the total number of fax machines demanded per month does not exceed 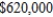 and the company has earmaked no more than $
and the company has earmaked no more than $ 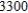 /month for manufacturing costs, how many units of each model should National make each month to maximize its monthly profit?
/month for manufacturing costs, how many units of each model should National make each month to maximize its monthly profit?
(Multiple Choice)
4.8/5  (41)
(41)
Solve the linear programming problem by the method of corners.
Find the maximum and minimum of 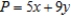 subject to
subject to 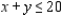
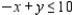
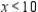
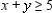
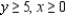 Max: x = __________; y = __________; P = __________
Min: x = __________; y = __________; P = __________
Max: x = __________; y = __________; P = __________
Min: x = __________; y = __________; P = __________
(Essay)
4.8/5  (30)
(30)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 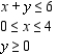
(Multiple Choice)
4.9/5  (34)
(34)
Solve the linear programming problem by the method of corners. Find the maximum and minimum of 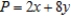 subject to
subject to 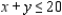
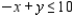
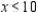
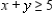
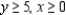
(Multiple Choice)
4.7/5  (33)
(33)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 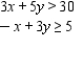
(Multiple Choice)
4.9/5  (30)
(30)
Formulate but do not solve the following exercise as a linear programming problem. A company manufactures products A, B, and C. Each product is processed in three departments: I, II, and III. The total available labor-hours per week for departments I, II, and III are 970, 1,090, and 860, respectively. The time requirements (in hours per unit) and profit per unit for each product are as follows:  How many units of each product should the company produce in order to maximize its profit?
How many units of each product should the company produce in order to maximize its profit?
(Multiple Choice)
4.8/5  (40)
(40)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 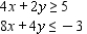
(Multiple Choice)
4.9/5  (39)
(39)
A veterinarian has been asked to prepare a diet for a group of dogs to be used in a nutrition study at the School of Animal Science. It has been stipulated that each serving should be no larger than 8 oz and must contain at least 29 units of nutrient I and 20 units of nutrient II. The vet has decided that the diet may be prepared from two brands of dog food: brand A and brand B. Each ounce of brand A contains 3 units of nutrient I and 4 units of nutrient II. Each ounce of brand B contains 5 units of nutrient I and 2 units of nutrient II. Brand A costs 6 cents/ounce and brand B costs 8 cents/ounce. Determine how many ounces of each brand of dog food should be used per serving to meet the given requirements at a minimum cost.
__________ ounces of brand A and __________ ounces of brand B
(Essay)
4.9/5  (33)
(33)
Perth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $14,000/day to operate, and it yields 50 oz of gold and 3,000 oz of silver each day. The Horseshoe Mine costs $16,000/day to operate, and it yields 75 oz of gold and 1,000 oz of silver each day. Company management has set a target of at least 650 oz of gold and 18,000 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost?
Saddle Mine: __________ days; Horseshoe Mine: __________ days
What is the minimum cost? $ __________
(Essay)
4.8/5  (36)
(36)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 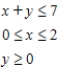
(Multiple Choice)
4.8/5  (40)
(40)
Solve the linear programming problem by the method of corners. Maximize 
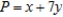 subject to
subject to 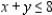
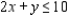
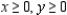
(Multiple Choice)
5.0/5  (39)
(39)
Formulate but do not solve the following exercise as a linear programming problem. Steinwelt Piano manufactures uprights and consoles in two plants, plant I and plant II. The output of plant I is at most 300/month, whereas the output of plant II is at most 250/month. These pianos are shipped to three warehouses that serve as distribution centers for the company. To fill current and projected future orders, warehouse A requires a minimum of 150 pianos/month, warehouse B requires at least 200 pianos/month, and warehouse C requires at least 200 pianos/month. The shipping cost of each piano from plant I to warehouse A, warehouse B, and warehouse C is $60, $30, and $50, respectively, and the shipping cost of each piano from plant II to warehouse A, warehouse B, and warehouse C is $90, $50, and $40, respectively. What shipping schedule will enable Steinwelt to meet the warehouses' requirements while keeping shipping costs to a minimum?
(Multiple Choice)
4.7/5  (28)
(28)
Showing 61 - 80 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)