Exam 22: Linear Programming
Exam 1: Operations and Productivity126 Questions
Exam 2: Operations Strategy in a Global Environment135 Questions
Exam 3: Project Management122 Questions
Exam 4: Forecasting144 Questions
Exam 5: Design of Goods and Services137 Questions
Exam 6: Managing Quality130 Questions
Exam 18: Statistical Process Control156 Questions
Exam 7: Process Strategy and Sustainability131 Questions
Exam 19: Capacity and Constraint Management107 Questions
Exam 8: Location Strategies140 Questions
Exam 9: Layout Strategies161 Questions
Exam 10: Human Resources,job Design,and Work Measurement192 Questions
Exam 11: Supply-Chain Management145 Questions
Exam 20: Outsourcing As a Supply-Chain Strategy73 Questions
Exam 12: Inventory Management171 Questions
Exam 13: Aggregate Planning134 Questions
Exam 14: Material Requirements Planning Mrpand Erp169 Questions
Exam 15: Short-Term Scheduling139 Questions
Exam 16: Jit and Lean Operations138 Questions
Exam 17: Maintenance and Reliability130 Questions
Exam 21: Decision-Making Tools97 Questions
Exam 22: Linear Programming100 Questions
Exam 23: Transportation Models94 Questions
Exam 24: Waiting-Line Models135 Questions
Exam 25: Learning Curves111 Questions
Exam 26: Simulation92 Questions
Select questions type
A feedlot is trying to decide on the lowest cost mix that will still provide adequate nutrition for its cattle.Suppose that the numbers in the chart represent the number of grams of ingredient per 100 grams of feed and that the cost of Feed X is $5/100grams,Feed Y is $3/100grams,and Feed X is $8/100 grams.Each cow will need 50 grams of A per day,20 grams of B,30 grams of C,and 10 grams of D.If the feedlot can get no more than 200 grams per day per cow of any of the feed types determine the constraints governing the problem.
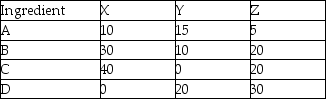
(Essay)
4.9/5  (29)
(29)
A linear programming problem contains a restriction that reads "the quantity of X must be at least twice as large as the quantity of Y." Formulate this as a constraint ready for use in problem solving software.
(Essay)
4.9/5  (30)
(30)
For the constraints given below,which point is in the feasible region of this maximization problem? (1)14x + 6y < 42 (2)x - y < 3 (3)x,y ≥ 0
(Multiple Choice)
4.8/5  (35)
(35)
What are corner points? What is their relevance to solving linear programming problems?
(Essay)
4.7/5  (43)
(43)
In linear programming,a statement such as "maximize contribution" becomes an objective function when the problem is formulated.
(True/False)
4.8/5  (39)
(39)
Suppose that an iso-profit line is given to be X + Y = 15.What would be the profit made from producing 20X and 10Y?
(Multiple Choice)
4.8/5  (33)
(33)
The ________ is the set of all feasible combinations of the decision variables.
(Essay)
5.0/5  (29)
(29)
In a linear programming problem,what is the relationship between the constraints and the feasible region? Explain with reference to a problem with two variables.
(Essay)
4.8/5  (35)
(35)
In linear programming,if there are three constraints,each representing a resource that can be used up,the optimal solution must use up all of each of the three resources.
(True/False)
4.7/5  (30)
(30)
Rienzi Farms grows sugar cane and soybeans on its 500 acres of land.An acre of soybeans brings a $1000 contribution to overhead and profit;an acre of sugar cane has a contribution of $2000.Because of a government program no more than 200 acres may be planted in soybeans.During the planting season 1200 hours of planting time will be available.Each acre of soybeans requires 2 hours,while each acre of sugar cane requires 5 hours.The company seeks maximum contribution (profit)from its planting decision.
a.Algebraically state the decision variables,objective and constraints.
b.Plot the constraints
c.Solve graphically,using the corner-point method. 
(Essay)
4.7/5  (34)
(34)
The property manager of a city government issues chairs,desks,and other office furniture to city buildings from a centralized distribution centre.Like most government agencies,it operates to minimize its costs of operations.In this distribution centre,there are two types of standard office chairs,Model A and Model B.Model A is considerably heavier than Model B,and costs $20 per chair to transport to any city building;each model B costs $14 to transport.The distribution centre has on hand 400 chairs-200 each of A and B.
The requirements for shipments to each of the city's buildings are as follows:
Building 1 needs at least 100 of A
Building 2 needs at least 150 of B.
Building 3 needs at least 100 chairs,but they can be of either type,mixed.
Building 4 needs 40 chairs,but at least as many B as A.
Write out the objective function and the constraints for this problem.(Hint: there are eight variables-chairs for building 1 cannot be used to satisfy the demands for another building).
(Essay)
4.8/5  (33)
(33)
The requirements of linear programming problems include an objective function,the presence of constraints,objective and constraints expressed in linear equalities or inequalities,and ________.
(Essay)
4.8/5  (39)
(39)
What combination of x and y will yield the optimum for this problem? Minimize $3x + $15y,subject to (1)2x + 4y < 12 and (2)5x + 2y < 10 and (3)x,y ≥ 0.
(Multiple Choice)
4.8/5  (26)
(26)
Which of the following is not a requirement of a linear programming problem?
(Multiple Choice)
4.8/5  (46)
(46)
In sensitivity analysis,a zero shadow price (or dual value)for a resource ordinarily means that the resource has not been used up.
(True/False)
4.8/5  (31)
(31)
A maximizing linear programming problem has two constraints: 2X + 4Y < 100 and 3X + 10Y < 210,in addition to constraints stating that both X and Y must be nonnegative.The corner points of the feasible region of this problem are
(Multiple Choice)
4.9/5  (37)
(37)
Showing 41 - 60 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)