Exam 4: The Derivative in Graphing and Applications
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
An object moves a distance s away from the origin according to the equation s(t) = 4t3 - 6t + 6, where 0 t 11. At what time is the object farthest from the origin?
(Multiple Choice)
4.8/5  (34)
(34)
Sketch the graph of y = x2/3(x - 7)2. Find any stationary points, inflection points, and cusps which may or may not exist. Approximate answers to 4 decimal places.
(Essay)
4.9/5  (40)
(40)
The position function of a particle is given by s = t(t - 7)2 for t 0. Find the functions for v and a.
(Essay)
4.7/5  (39)
(39)
Let s(t) = 5t5 -5t be a position function. Fund v when t = 2.
(Multiple Choice)
5.0/5  (30)
(30)
Given y = x1/3(x + 5). Find any stationary points and any inflections points.
(Essay)
4.7/5  (31)
(31)
The largest interval over which f is increasing for f(x) = (x -2)8 is
(Multiple Choice)
4.7/5  (37)
(37)
Determine the x-coordinate of each stationary point of f(x) = 6x2-36x.
(Multiple Choice)
4.9/5  (29)
(29)
The position function of a particle is given by s = 3t2 - 7t + 1 for t 0. Find the functions for v and a.
(Short Answer)
4.8/5  (31)
(31)
Verify that f(x) = x3 -3x2- 3x + 1 satisfies the hypothesis of the Mean-Value Theorem over the interval [0, 2] and find all values of C that satisfy the conclusion of the theorem.
(Essay)
4.8/5  (31)
(31)
Find the area of the largest possible isosceles triangle with 2 sides equal to 12.
(Essay)
4.8/5  (29)
(29)
Answer true or false. This can be the graph of a particle's position if the particle is moving to the right at t = 3. 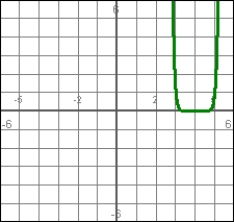
(True/False)
4.8/5  (40)
(40)
Use a graphing utility to estimate the absolute maximum of f(x) = (x - 3)2 on [-1, 5], if it exists.
(Multiple Choice)
4.8/5  (30)
(30)
Use Newton's Method to find the x-coordinate of the intersection of y = x4 + 2x3 and y = 2x2 + 2x + 1.
(Multiple Choice)
4.9/5  (26)
(26)
If f(x) = x(x- 7)5 , find the intervals where f is concave up and where f is concave down.
(Essay)
4.9/5  (30)
(30)
Given f(x) = 4x3 -6x2 - 4x + 10, find the intervals where f is concave up and where f is concave down.
(Essay)
4.9/5  (41)
(41)
The position function of a particle is given by s(t) = 3t + sin 3t. Find the acceleration function.
(Short Answer)
4.8/5  (30)
(30)
If f(x) = 2x4 -11x3 + 44 , find the location of any inflection points.
(Essay)
4.8/5  (31)
(31)
Showing 201 - 220 of 656
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)