Exam 4: The Derivative in Graphing and Applications
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Approximate 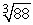 by applying Newton's Method to the equation x3 - 88 = 0. Use 4 for your initial value and calculate nine iterations.
by applying Newton's Method to the equation x3 - 88 = 0. Use 4 for your initial value and calculate nine iterations.
(Essay)
4.8/5  (27)
(27)
The stiffness of a beam of rectangular cross section is proportional to the product xy3. Find the stiffest beam which can be cut from a log with diameter d = 14 inches. See figure on right. 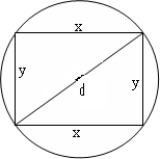
(Essay)
4.8/5  (45)
(45)
A sheet of cardboard 30 in square is used to make an open box by cutting squares of equal size from the corners and folding up the sides. What size squares should be cut to obtain a box with largest possible volume?
(Essay)
4.7/5  (18)
(18)
Determine the x-coordinate of each stationary point of f(x) = 3x2 -24x.
(Multiple Choice)
4.9/5  (37)
(37)
The position function of a particle is given by s(t) = 4t - 3t2 + 4t3. Find the velocity function.
(Short Answer)
5.0/5  (38)
(38)
If f(x) = (x - 7)4 + 3 , find the location of any inflection points.
(Short Answer)
4.9/5  (32)
(32)
A line is drawn through the point P(5, 2) so that it intersects the y-axis at A(0,y) and the x-axis at B(x,0). Find the smallest triangle formed if x and y are positive.
(Essay)
4.8/5  (32)
(32)
The largest interval over which f is increasing for f(x) = x9 - 5 is
(Multiple Choice)
4.7/5  (34)
(34)
Sketch the graph of y = 7x4 -7x3 + 2. Find any stationary points and any points of inflection.
(Essay)
4.8/5  (29)
(29)
Answer true or false. Using a graphing utility it can be shown that f(x) = x4 sin 4x has a relative maximum on 0 < x < 2 .
(True/False)
4.7/5  (38)
(38)
Answer true or false. A fence is to be used to enclose a rectangular plot of land. If there are 920 feet of fencing, it can be shown that a 230 ft by 230 ft square is the rectangle that can be enclosed with the greatest area. (A square is considered a rectangle.)
(True/False)
4.8/5  (39)
(39)
If f(x) = sin 2x (0, ), find the intervals where f is concave up and where f is concave down.
(Short Answer)
4.9/5  (39)
(39)
The position function of a particle is given by s(t) = 8t + cos t. Find the velocity function.
(Short Answer)
4.8/5  (29)
(29)
Verify that f(x) = x3 - 5x + 3 satisfies the hypothesis of the Mean-Value Theorem over the interval [-2, 3] and find all values of C that satisfy the conclusion of the theorem.
(Essay)
4.8/5  (30)
(30)
If f(x) = 3x4 -90x2 , find the intervals where f is concave up and where f is concave down.
(Essay)
4.9/5  (39)
(39)
Answer true or false. f(x) = | cot2x| has no relative extrema on 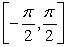 .
.
(True/False)
4.7/5  (31)
(31)
Given 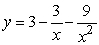 . Find any stationary points and any points of inflection. Also find any vertical and horizontal asymptotes.
. Find any stationary points and any points of inflection. Also find any vertical and horizontal asymptotes.
(Essay)
4.8/5  (33)
(33)
Let s(t) = t4 - 5t + 6 be a position function. The acceleration function a(t) =
(Multiple Choice)
4.8/5  (35)
(35)
Answer true or false. If f ''(-8) = -10 and f ''(8) = 10, then there must be a point of inflection on (-8, 8).
(True/False)
4.8/5  (39)
(39)
Showing 561 - 580 of 656
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)