Exam 4: The Derivative in Graphing and Applications
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Sketch the graph of y = x3 - 9x2 + 24x - 3. Find any minima, maxima, and inflection points.
(Essay)
4.8/5  (30)
(30)
Answer true or false. The Mean-Value Theorem can be used on f(x) = |x - 3| on [-5, 5].
(True/False)
4.9/5  (30)
(30)
Sketch the graph of y = x3 + 12x2. Find any stationary points and any points of inflection.
(Essay)
4.8/5  (36)
(36)
Sketch the graph of y = x3-48x + 4. Find any stationary points and any points of inflection.
(Essay)
4.9/5  (34)
(34)
A rectangle is to have an area of 32 in2. What should be its dimensions if the distance from one corner to the mid-point of a nonadjacent side is to be a minimum? 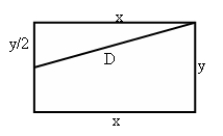
(Essay)
4.9/5  (19)
(19)
Find the dimensions of the rectangle of greatest area that can be inscribed in a circle of radius a.
(Essay)
4.8/5  (38)
(38)
Two numbers sum to 42. Find the two numbers whose product is maximum.
(Multiple Choice)
4.9/5  (35)
(35)
Use Rolle's Theorem to show that f(x) = 4x3 + 5x - 1 does not have more than one real root.
(Essay)
4.9/5  (39)
(39)
Sketch the graph of y = x4 -14x2 + 50. Find any extrema and any points of inflection.
(Essay)
4.9/5  (31)
(31)
If ![If on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)](https://storage.examlex.com/TB6988/11ead0bc_8ce6_b3c0_99a0_f911d6efbd9e_TB6988_11.jpg) on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)
on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)
(Multiple Choice)
4.8/5  (38)
(38)
Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for ![Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for on [0, 4 \pi ].](https://storage.examlex.com/TB6988/11ead0bc_8ce6_dad2_99a0_6143504b0922_TB6988_11.jpg) on [0, 4 ].
on [0, 4 ].
(True/False)
4.9/5  (30)
(30)
Sketch the graph of y = x2(9 -x2). Find any extrema and any points of inflection.
(Essay)
4.9/5  (32)
(32)
The equation, x3 - 4x - 17 = 0 has one real solution for 1 < x < 17. Approximate it by Newton's Method.
(Essay)
4.8/5  (37)
(37)
A rectangular garden is to be laid out with one side adjoining a neighbor's lot and is to contain 507ft2. If the neighbor agrees to pay for half the dividing fence, what should the dimensions of the garden be to insure a minimum cost of enclosure?
(Essay)
4.8/5  (35)
(35)
Let s(t) = t9 -t be a position function of a particle. At 1 the particle's acceleration is
(Multiple Choice)
4.9/5  (40)
(40)
Find the value of c in the interval [0, 1] that satisfies the Mean Value Theorem. f(x) = x4 + 8
(Essay)
4.8/5  (26)
(26)
Use Rolle's Theorem to prove that the equation 6x5 - 28x3 + 6 = 0 has at least one solution in the interval (0, 1).
(Essay)
4.8/5  (36)
(36)
Find the value c that satisfies Rolle's Theorem for f(x) = x3 - 4x on [-2, 2].
(Multiple Choice)
4.9/5  (39)
(39)
Showing 61 - 80 of 656
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)