Exam 4: The Derivative in Graphing and Applications
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Use a graphing utility to estimate the absolute minimum of f(x) = (ln x)(x - 3)2 on the interval (1, 5).
(Short Answer)
4.9/5  (40)
(40)
Find the relative extreme values for f(x) = x + sin x on the interval 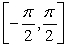 and determine where those values occur.
and determine where those values occur.
(Essay)
4.8/5  (28)
(28)
Verify that f(x) = x2 + 2 satisfies the hypothesis of the Mean-Value Theorem on the interval [0, 4] and find all values of C that satisfy the conclusion of the theorem.
(Essay)
4.9/5  (26)
(26)
Given y = x2/3(x + 6). Plot any stationary points, inflections points, and cusps which may or may not exist. Approximate answers to 4 decimal places.
(Essay)
4.9/5  (29)
(29)
For a triangle with sides 6 m, 8 m, and 10 m, the smallest circle that contains the triangle has a diameter of
(Multiple Choice)
4.9/5  (38)
(38)
Use a graphing utility to assist in determining the location of the absolute maximum of f(x) = -(x2 - 7)2 on (- , ), if it exists.
(Multiple Choice)
4.8/5  (39)
(39)
Find the relative extreme values for f(x) = 5x3 - 30x2 + 7 on the interval [-1, 10] and determine where those values occur.
(Essay)
5.0/5  (36)
(36)
Answer true or false. All functions of the form f(x) = axn , where n is odd and a 0 have an inflection point.
(True/False)
4.9/5  (44)
(44)
Given f(x) = -5x3 + 15x2 . Use a graphing utility to estimate the absolute maximum and minimum values of f, if any, on the interval [0, 3].
(Essay)
4.8/5  (26)
(26)
Find the extreme values for f(x) = x - sin 4x on the interval 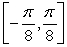 and determine where those values occur.
and determine where those values occur.
(Essay)
5.0/5  (37)
(37)
Sketch the graph of 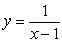 . Identify the vertical and horizontal asymptotes.
. Identify the vertical and horizontal asymptotes.
(Essay)
4.7/5  (33)
(33)
Find the relative extreme values for f(x) = 3x3 -18x2 + 2 on the interval [-1, 10] and determine where those values occur.
(Essay)
4.9/5  (25)
(25)
The strength of a beam with a rectangular cross section varies directly as x and as the square of y. What are the dimensions of the strongest beam that can be sawed out of a round log whose diameter is d = 27 inches? See figure on right. 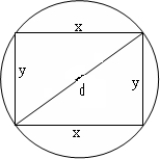
(Essay)
4.9/5  (36)
(36)
Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for ![Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for on [-1, 1].](https://storage.examlex.com/TB6988/11ead0bc_8d44_8b9d_99a0_23d3afa1fcf5_TB6988_11.jpg) on [-1, 1].
on [-1, 1].
(True/False)
4.8/5  (40)
(40)
Express the number 54 as the sum of two nonnegative numbers whose product is as large as possible.
(Multiple Choice)
4.8/5  (39)
(39)
The cost of fuel used in propelling a dirigible varies as the square of its speed and is $100/hour when the speed is 100 miles/hour. Other expenses amount to $200/hour. Find the most economical speed for a voyage of 1,400 miles.
(Essay)
4.7/5  (35)
(35)
A lighthouse is 8 miles off a straight coast and a town is located 18 miles down the seacoast. Supplies are to be moved from the town to the lighthouse on a regular basis and at a minimum time. If the supplies can be moved at the rate of 7 miles/hour on water and 25 miles/hour over land, how far from the town should a dock be constructed for shipment of supplies? 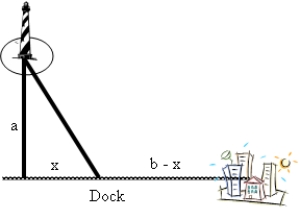
(Essay)
4.9/5  (41)
(41)
Showing 81 - 100 of 656
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)