Exam 4: The Derivative in Graphing and Applications
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Use a graphing utility to estimate the absolute maximum of ![Use a graphing utility to estimate the absolute maximum of on [-2, 2].](https://storage.examlex.com/TB6988/11ead0bc_8d27_b47c_99a0_af6a5e598859_TB6988_11.jpg) on [-2, 2].
on [-2, 2].
(Short Answer)
5.0/5  (44)
(44)
Find the extreme values for 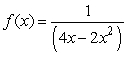 on the interval (0, 2) and determine where those values occur.
on the interval (0, 2) and determine where those values occur.
(Essay)
4.9/5  (30)
(30)
Use a graphing utility to estimate the absolute minimum of f(x) = ln(x8) on [1, 3].
(Short Answer)
4.8/5  (30)
(30)
If f(x) = x4 - 4x2, find the intervals where f is increasing and where f is decreasing.
(Essay)
4.7/5  (27)
(27)
Answer true or false. f(x) = | sec2x| has no relative extrema on 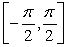 .
.
(True/False)
4.8/5  (28)
(28)
f(x) = 9x4 - 7x5 , find the intervals where f is increasing and where f is decreasing.
(Essay)
4.7/5  (31)
(31)
A company has a cost of operation function given by C(t) = 0.02t2 - 2t + 5,000 for 0 t 500. Find the minimum cost of operation.
(Multiple Choice)
4.8/5  (37)
(37)
A can containing 13.5 in3 of tuna and water is to be made in the form of a circular cylinder. What dimensions of the can will require the least amount of material? (V = r2h, S = 2 rh, A = r2)
(Essay)
4.9/5  (40)
(40)
Use Newton's Method to find the largest positive solution of x4 + x3 -4x2- 4x - 7 = 0.
(Multiple Choice)
4.9/5  (41)
(41)
Sketch the graph of 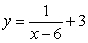 . Find any stationary points and any points of inflection. Also find any vertical and horizontal asymptotes.
. Find any stationary points and any points of inflection. Also find any vertical and horizontal asymptotes.
(Essay)
4.9/5  (35)
(35)
Two fences, a distance of d = 16 feet apart are to be constructed so that the first fence is a height of h = 2 feet high and the second fence is higher than the first. What is the length of the shortest pole that has one end on the ground, passing over the first fence and reaches the second fence? See figure. 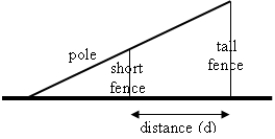
(Essay)
4.7/5  (34)
(34)
Answer true or false. The Mean-Value Theorem guarantees there is at least one c on [0, 3] such that f '(x) = 0.9 when f(x) = x.
(True/False)
4.7/5  (39)
(39)
Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for f(x) = cos 2x on [0, 4 ].
(True/False)
4.7/5  (35)
(35)
Answer true or false. A point that has an x-coordinate where f ''(x) = 0 is a point of inflection.
(True/False)
4.7/5  (35)
(35)
f(x) = 4x4 - 9x5 , find the intervals where f is increasing and where f is decreasing.
(Essay)
4.9/5  (27)
(27)
The position function of a particle is given by s(t) = 9t - 9. Find the velocity function.
(Short Answer)
4.8/5  (35)
(35)
On a [-10, 10] by [-10, 10] window on a graphing utility the rational function ![On a [-10, 10] by [-10, 10] window on a graphing utility the rational function has](https://storage.examlex.com/TB6988/11ead0bc_8d3a_0407_99a0_17e2e7e62d27_TB6988_11.jpg) has
has
(Multiple Choice)
4.8/5  (33)
(33)
Showing 141 - 160 of 656
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)