Exam 4: The Derivative in Graphing and Applications
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
The equation, x3 - x2 - 4x - 4 = 0 has one real solution for 1 < x < 4. Approximate it by Newton's Method. Use 3 for your initial value and calculate eight iterations.
(Essay)
4.8/5  (36)
(36)
An isosceles triangle is drawn with its vertex at the origin and its base parallel to the x axis. The vertices of the base are on the curve 6y = 30 - x2. Find the area of the largest such triangle.
(Essay)
4.7/5  (26)
(26)
Verify that f(x) = x3 -5x + 4 satisfies the hypothesis of the Mean-Value Theorem over the interval [-2, 3] and find all values of C that satisfy the conclusion of the theorem.
(Essay)
4.8/5  (44)
(44)
Given f(x) = 20x3 -12x2 - 3x + 9, find the intervals where f is concave up and where f is concave down.
(Essay)
4.8/5  (35)
(35)
If f(x) = x(x - 7)5 , find the intervals where f is concave up and where f is concave down.
(Essay)
4.9/5  (30)
(30)
Sketch the graph of y = 4 - 2x- x2. Find any stationary points and any points of inflection.
(Essay)
4.8/5  (34)
(34)
If f(x) = x4 - 19x3 + 39 , find the location of any inflection points.
(Essay)
4.8/5  (37)
(37)
Answer true or false. If a particle is dropped a distance of 619 m. It has a speed of 110.16 m/s (rounded to the nearest hundredth of a m/s) when it hits the ground.
(True/False)
4.7/5  (27)
(27)
Does ![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8cea_8478_99a0_55cf175bbf91_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.
(Essay)
4.9/5  (43)
(43)
Find the value of c in the interval [0, 2 ] that satisfies the Mean Value Theorem. f(x) = 6 cos x
(Essay)
4.7/5  (30)
(30)
Sketch the graph of 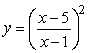 . Find any stationary points and any points of inflection. Also find any horizontal and vertical asymptotes.
. Find any stationary points and any points of inflection. Also find any horizontal and vertical asymptotes.
(Essay)
4.8/5  (39)
(39)
Does ![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.](https://storage.examlex.com/TB6988/11ead0bc_8d34_fac8_99a0_8d527b07ee5a_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.
(Essay)
4.8/5  (33)
(33)
Given the position function s = 2t3 -6t2 + 5t + 4; find s and v when a = 0 (Where v is the velocity and a is the acceleration.).
(Essay)
4.9/5  (35)
(35)
Use Newton's Method to find the largest positive solution of x5 + 6x3-3x2 - 9 = 0. Use 3 for your initial value and calculate three iterations.
(Multiple Choice)
4.8/5  (36)
(36)
Answer true or false. ![Answer true or false. on [-2, 2] satisfies the hypotheses of Rolle's Theorem.](https://storage.examlex.com/TB6988/11ead0bc_8d44_8b9c_99a0_cbfebf57ef14_TB6988_11.jpg) on [-2, 2] satisfies the hypotheses of Rolle's Theorem.
on [-2, 2] satisfies the hypotheses of Rolle's Theorem.
(True/False)
4.8/5  (41)
(41)
Use Newton's Method to find the largest solution of x5 - 2x4 + 5x3 -x2 + 7x + 12 = 0. Use 2 for your initial value and calculate six iterations.
(Multiple Choice)
4.8/5  (34)
(34)
The derivative of a continuous function is f '(x) = 4(x -7)2(4x + 4). Find all critical points and determine whether a relative maximum, relative minimum or neither occurs there.
(Essay)
5.0/5  (31)
(31)
A divided field is to be constructed with 7640 feet of fence as shown.
For what value of x will the area be a maximum? 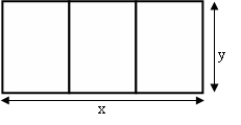
(Short Answer)
4.9/5  (30)
(30)
Showing 581 - 600 of 656
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)