Exam 4: The Derivative in Graphing and Applications
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Find the value of c in the interval [0, 4] that satisfies the Mean Value Theorem. f(x) = 5x2 + 20
(Essay)
4.7/5  (42)
(42)
Given the position function s = 2t3 - 12t2 ; find s and v when a = 0 (Where v is the velocity and a is the acceleration.).
(Essay)
4.9/5  (42)
(42)
Use Rolle's Theorem to show that f(x) = 2x3 + 2x - 6 does not have more than one real root.
(Essay)
4.8/5  (47)
(47)
Given f(x) = -x5 + 15x4 . Use a graphing utility to estimate the absolute maximum and minimum values of f, if any, on the interval [0, 15].
(Essay)
4.9/5  (42)
(42)
If f(x) = x4 . Use a graphing utility to estimate the absolute maximum and minimum values of f, if any, on the interval [-1, 2].
(Essay)
4.8/5  (32)
(32)
Given f(x) = -2x5 + 20x2 . Use a graphing utility to estimate the absolute maximum and minimum values of f, if any, on the interval [0, 3].
(Essay)
4.9/5  (39)
(39)
Verify that f(x) = x3 - x satisfies the hypothesis of Rolle's Theorem on the interval [-1, 1] and find all values of C in (-1, 1) such that f '(C) = 0
(Essay)
4.9/5  (35)
(35)
The graph represents a velocity function. The acceleration at t = 2 is 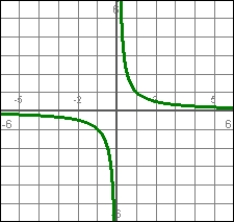
(Multiple Choice)
4.8/5  (27)
(27)
Sketch the graph of 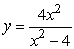 . Find any stationary points and any points of inflection. Also find any horizontal and vertical asymptotes.
. Find any stationary points and any points of inflection. Also find any horizontal and vertical asymptotes.
(Essay)
4.8/5  (37)
(37)
If f(x) = x(x + 2)3 , find the intervals where f is increasing and where f is decreasing.
(Essay)
4.8/5  (39)
(39)
Use Rolle's Theorem to prove that the equation 8x7 - 16x3 + 3 = 0 has at least one solution in the interval (0, 1).
(Essay)
5.0/5  (35)
(35)
Find the value of c in the interval [0, ] that satisfies the Mean Value Theorem. f(x) = sin(8x)
(Essay)
4.9/5  (36)
(36)
Use a graphing utility to estimate the absolute minimum of f(x) = x4e x on [-1, 1].
(Short Answer)
4.7/5  (19)
(19)
Find the dimensions of the rectangle of maximum area which may be embedded in a right triangle with base of 5, height of 12, and hypotenuse of 13 feet as shown in the figure. 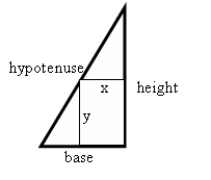
(Short Answer)
4.8/5  (34)
(34)
If f(x) = 4x4 - 9x3 , find the intervals where f is concave up and where f is concave down.
(Essay)
4.7/5  (28)
(28)
If f(x) = 6x4 - 24x3 + 5 , find the intervals where f is increasing and where f is decreasing.
(Essay)
4.9/5  (32)
(32)
Showing 301 - 320 of 656
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)