Exam 12: Limits and An Introduction To Calculus
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Find a formula for the slope of the graph of at the point .Then use it to find the slope at the given point.
(Multiple Choice)
4.9/5  (42)
(42)
Use the position function to find the velocity in feet/second at time seconds.The velocity at time seconds is given by .
(Multiple Choice)
5.0/5  (40)
(40)
Graph the function.Determine the limit (if it exists)by evaluating the corresponding one-sided limits.
(Multiple Choice)
4.8/5  (38)
(38)
Select the correct graph for the following function using a graphing utility.
(Multiple Choice)
4.7/5  (36)
(36)
Select the correct function for the graph using oblique asymptotes as aids. 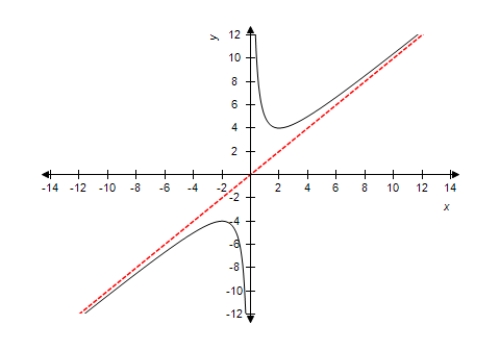
(Multiple Choice)
4.9/5  (36)
(36)
Determine (if it exists)by evaluating the corresponding one-sided limits.
(Multiple Choice)
4.8/5  (37)
(37)
Use the limit process to find the area of the region between the graph of the function and the x-axis over the specified interval.
Function Interval f(x)=8x- [0,1]
(Multiple Choice)
4.8/5  (34)
(34)
Approximate the area of the indicated region under the given curve using five rectangles. 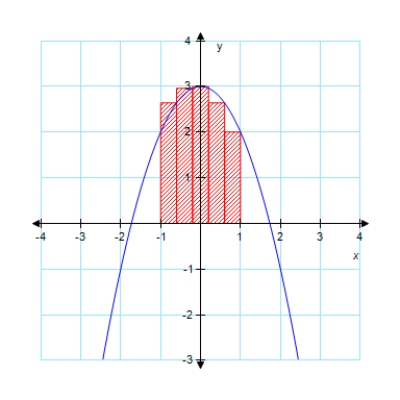
(Multiple Choice)
4.9/5  (31)
(31)
Determine (if it exists)by evaluating the corresponding one-sided limits.
(Multiple Choice)
4.8/5  (23)
(23)
Find a formula for the slope of the graph of at the point .Then use it to find the slope at the given point.
(Multiple Choice)
4.9/5  (32)
(32)
Use the limit process to find the area of the region between and the x-axis on the interval [1,8].Round your answer upto 1 decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Use the slope to find an equation of the tangent line to the graph at the given point.
(Multiple Choice)
4.9/5  (31)
(31)
Showing 221 - 240 of 259
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)