Exam 12: Limits and An Introduction To Calculus
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Use the function and its derivative to determine any points on the graph of at which the tangent line is horizontal.Use a graphing utility to verify your results.
(Multiple Choice)
4.9/5  (32)
(32)
Use the graph to determine the limit visually (if it exists).Then identify another function g2(x)that agrees with the given function at all but one point.
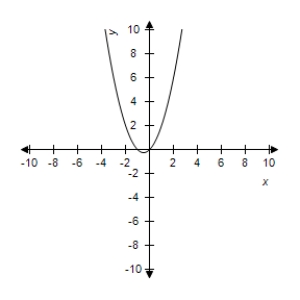
(Multiple Choice)
4.9/5  (38)
(38)
Select the correct graph for the following function using a graphing utility.
(Multiple Choice)
4.8/5  (38)
(38)
Algebraically evaluate the limit (if it exists)by the appropriate technique(s).
(Multiple Choice)
4.9/5  (33)
(33)
Use the limit process to find the slope of the graph of at .
(Multiple Choice)
4.8/5  (29)
(29)
Graphically approximate the limit (if it exists)by using a graphing utility to graph the function.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 241 - 259 of 259
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)