Exam 9: Hypothesis Testing
Exam 1: Introduction to Business Analytics29 Questions
Exam 2: Describing the Distribution of a Single Variable100 Questions
Exam 3: Finding Relationships Among Variables85 Questions
Exam 4: Probability and Probability Distributions114 Questions
Exam 5: Normal, Binomial, Poisson, and Exponential Distributions125 Questions
Exam 6: Decision Making Under Uncertainty107 Questions
Exam 7: Sampling and Sampling Distributions90 Questions
Exam 8: Confidence Interval Estimation84 Questions
Exam 9: Hypothesis Testing87 Questions
Exam 10: Regression Analysis: Estimating Relationships92 Questions
Exam 11: Regression Analysis: Statistical Inference82 Questions
Exam 12: Time Series Analysis and Forecasting106 Questions
Exam 13: Introduction to Optimization Modeling97 Questions
Exam 14: Optimization Models114 Questions
Exam 15: Introduction to Simulation Modeling82 Questions
Exam 16: Simulation Models102 Questions
Exam 17: Data Mining20 Questions
Exam 18: Importing Data Into Excel19 Questions
Exam 19: Analysis of Variance and Experimental Design20 Questions
Exam 20: Statistical Process Control20 Questions
Select questions type
The owner of a popular Internet-based auction site believes that more than half of the people who sell items on her site are women. To test this hypothesis, the owner sampled 1000 customers who sold items on her site and she found that 53% of the customers sampled were women. Some calculations are shown in the table below.  -(A) If you were to conduct a hypothesis test to determine if greater than 50% of customers who use this Internet-based site are women, would you conduct a one-tail or a two-tail hypothesis test? Explain your answer, and state the appropriate null and alternative hypotheses.
(B) How many customers out of the 1000 sampled must have been women in this case?
(C) Using a 5% significance level, can the owner of this site conclude that women make up more than 50% of her customers? Explain your answer.
(D) If you were to use a 1% significance level, would the conclusion from (C) change? Explain your answer.
-(A) If you were to conduct a hypothesis test to determine if greater than 50% of customers who use this Internet-based site are women, would you conduct a one-tail or a two-tail hypothesis test? Explain your answer, and state the appropriate null and alternative hypotheses.
(B) How many customers out of the 1000 sampled must have been women in this case?
(C) Using a 5% significance level, can the owner of this site conclude that women make up more than 50% of her customers? Explain your answer.
(D) If you were to use a 1% significance level, would the conclusion from (C) change? Explain your answer.
(Essay)
4.9/5  (33)
(33)
Type I errors are usually considered more "costly" although this can lead to conservative decision making.
(True/False)
4.9/5  (32)
(32)
Side-by-side box-plots are typically a good way to begin the analysis when comparing two populations.
(True/False)
4.7/5  (40)
(40)
The p-value of a sample is the probability of seeing a sample with
(Multiple Choice)
4.7/5  (35)
(35)
The power of a test is the probability of rejecting the null hypothesis when the alternative hypothesis is true.
(True/False)
4.7/5  (43)
(43)
An automobile manufacturer needs to buy aluminum sheets with an average thickness of 0.05 inch. The manufacturer collects a random sample of 40 sheets from a potential supplier. The thickness of each sheet in this sample is measured (in inches) and recorded. The information below are pertaining to the Chi-square goodness-of-fit test.  -(A) Are these measurements normally distributed? Summarize your results.
(B) Are there any weaknesses or concerns about your conclusions in (A)? Explain
-(A) Are these measurements normally distributed? Summarize your results.
(B) Are there any weaknesses or concerns about your conclusions in (A)? Explain
(Essay)
4.7/5  (38)
(38)
The null and alternative hypotheses divide all possibilities into:
(Multiple Choice)
4.8/5  (38)
(38)
An investor wants to compare the risks associated with two different stocks. One way to measure the risk of a given stock is to measure the variation in the stock's daily price changes. The investor obtains a random sample of 20 daily price changes for stock 1 and 20 daily price changes for stock 2. These data are shown in the table below. Show how this investor can compare the risks associated with the two stocks by testing the null hypothesis that the variances of the stocks are equal. Use 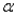 = 0.10 and interpret the results of the statistical test.
= 0.10 and interpret the results of the statistical test. 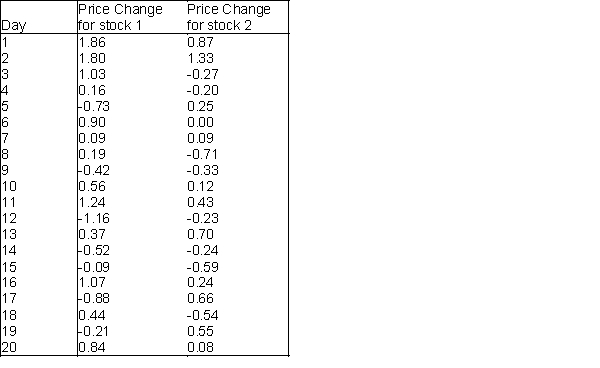
(Essay)
4.9/5  (35)
(35)
The chi-square test for normality makes a comparison between the observed histogram and a histogram based on normality.
(True/False)
4.8/5  (39)
(39)
(A) Assume that the national average weekly grocery bill for a five-person family is $131. Is the sample evidence statistically significant? If so, at what significance levels can you reject the null hypothesis?
(B) For which values of the sample mean (i.e., average weekly grocery bill) would you decide to reject the null hypothesis at the 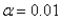 significance level? For which values of the sample mean would you decide to reject the null hypothesis at the 10% level of significance?
significance level? For which values of the sample mean would you decide to reject the null hypothesis at the 10% level of significance?
(Essay)
5.0/5  (36)
(36)
A null hypothesis is a statement about the value of a population parameter. It is usually the current thinking, or "status quo".
(True/False)
4.8/5  (44)
(44)
Q-Mart is interested in comparing customers who used its own charge card with those who use other types of credit cards. Q-Mart would like to know if customers who use the Q-Mart card spend more money per visit, on average, than customers who use some other type of credit card. They have collected information on a random sample of 38 charge customers and the data is presented below. On average, the person using a Q-Mart card spends $192.81 per visit and customers using another type of card spend $104.47 per visit. 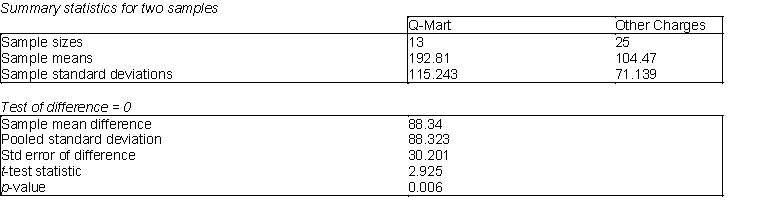 -(A) Given the information above, what is
-(A) Given the information above, what is 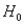 and
and 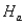 for this comparison? Also, does this represent a one-tailed or a two-tailed test? Explain your answer.
(B) What are the degrees of freedom for the t-statistic in this calculation? Explain how you would calculate the degrees of freedom in this case.
(C) What is the assumption in this case that allows you to use the pooled standard deviation for this test?
(D) Using a 5% level of significance, is there sufficient evidence for Q-Mart to conclude that customers who use the Q-Mart card charge, on average, more than those who use another charge card? Explain your answer.
(E) Using a 1% level of significance, is there sufficient evidence for Q-Mart to conclude that customers who use the Q-Mart card charge, on average, more than those who use another charge card? Explain your answer.
for this comparison? Also, does this represent a one-tailed or a two-tailed test? Explain your answer.
(B) What are the degrees of freedom for the t-statistic in this calculation? Explain how you would calculate the degrees of freedom in this case.
(C) What is the assumption in this case that allows you to use the pooled standard deviation for this test?
(D) Using a 5% level of significance, is there sufficient evidence for Q-Mart to conclude that customers who use the Q-Mart card charge, on average, more than those who use another charge card? Explain your answer.
(E) Using a 1% level of significance, is there sufficient evidence for Q-Mart to conclude that customers who use the Q-Mart card charge, on average, more than those who use another charge card? Explain your answer.
(Essay)
4.8/5  (38)
(38)
An insurance firm interviewed a random sample of 600 college students to find out the type of life insurance preferred, if any. The results are shown in the table below. Is there evidence that life insurance preference of male students is different than that of female students. Test at the 5% significance level. 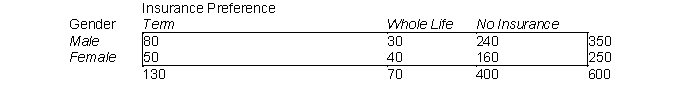
(Essay)
4.9/5  (39)
(39)
When testing the equality of two population variances, the test statistic is the ratio of the population variances; namely 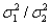 .
.
(True/False)
4.8/5  (47)
(47)
A sport preference poll yielded the following data for men and women. Use the 5% significance level and test to determine if sport preference and gender are independent. 
(Essay)
4.8/5  (28)
(28)
Showing 41 - 60 of 87
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)