Exam 7: Sampling and Sampling Distributions

The finite population correction factor, 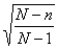, should generally be used when:

We can measure the accuracy of judgmental samples by applying some simple rules of probability. This way, judgmental samples are not likely to contain our built-in biases.

The manager of a local fast-food restaurant is interested in improving service provided to customers who use the restaurant's drive-up window. As a first step in the process, the manager asks his assistant to record the time (in minutes) it takes to serve a large number of customers at the final window in the facility's drive-up system. The given frame in this case is 200 customer service times observed during the busiest hour of the day for this fast-food restaurant. The frame of 200 service times yielded a mean of 0.881. A simple random sample of 10 from this frame is presented below. -(A) What sample size would be required for the production personnel to be approximately 95% sure that their estimate of the average number of defective batteries per box is within 0.3 unit of the true mean? Assume that the best estimate of the population standard deviation ( 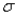) is 0.9 defective batteries per box. (B) How does your answer to (A) change if the production personnel want their estimate to be within 0.5 unit of the actual population mean? Evaluate the tradeoff between required accuracy and sample size requirement for this case and the case in (A).

The defining property of a simple random sample is that:

The opportunity for nonsampling error is increased by:

If the sample size is greater than 30, the Central Limit Theorem (CLT) will always apply.

The two basic sources for error when using random sampling are:

One obvious advantage of stratified sampling is that we obtain separate estimates within each stratum - which we would not obtain if we took a simple random sample from the entire population. A more important advantage is that we can increase the accuracy of the resulting population estimates by using appropriately defined strata.

When the sample size is greater than 5% of the population, the formula for the standard error of the mean should be modified with a finite population correction.

Which of the following are reasons for why simple random sampling is used infrequently in real applications?

In sampling, a population is:

Estimation is the process of inferring the value of an unknown population parameter using data from a random sample

A list of all members of the population is called a:

A columnist for the LA Times is working to meet a deadline on a story about commuting in Los Angeles. She wants to include information about the current price of gasoline in the Los Angeles metro area, but her source person for this type of information has already gone home for the day. So she decides to take her own sample as she drives home, writing down the prices she observes as she makes her way from downtown to her neighborhood in the suburbs. Below is the data sample she obtains (units are $/gallon). 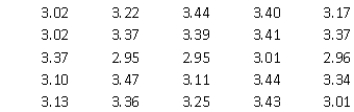-(A) Do you think she has obtained a true random sample? ​ (B) What average price could she report, based on the above sample? ​ (C) What average price range could she report, based on the above sample? ​ (D) Do you see any issues with reporting the range calculated for (C)?

A sales manager for a company that makes commercial ovens for restaurants is interested in estimating the average number of restaurants in all metropolitan areas across the entire country. He does not have access to the data for each metropolitan location, so he had decided to select a sample that will be representative of all such areas, and will use a sample size of 30. Do you believe that simple random sampling is the best approach to obtaining a representative subset of the metropolitan areas in the given frame? Explain. If not, recommend how the sales manager might proceed to select a better sample of size 30 from this data?

The mean of the sampling distribution of always equals:

Simple random sampling can result in under-representation or over-representation of certain segments of the population. This is one of several reasons that simple random samples are almost never used in real applications.

Which of the following statements correctly describe estimation?

A sample chosen in such a way that every possible subset of same size has an equal chance of being selected is called a(n):

A sample of size 20 is selected at random from a population of size N. If the finite population correction factor is 0.9418, then N must be 169.