Exam 18: Nonparametric Methods

Three universities in your state have decided to administer the same comprehensive examination to the recipients of MBA degrees. From each institution, a random sample of MBA recipients has been selected and given the test. The following table shows the scores of the students from each university. Use the Kruskal-Wallis test to determine if there is a significant difference in the average scores of the students from the three universities. Let $\alpha$ = 0.01.

Two faculty members ranked 12 candidates for scholarships. Calculate the Spearman rank-correlation coefficient and test it for significance. Use a .02 level of significance.

Two faculty members (X and Y) ranked five candidates for scholarships. The rankings are shown below. 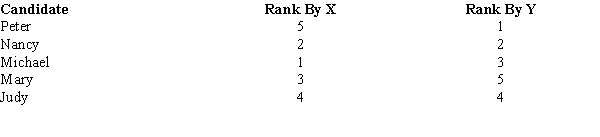Compute the Spearman rank-correlation and test it for significance. Let $\alpha$ = 0.05.

If a null hypothesis that states that two populations are identical is rejected using a nonparametric test, then it is safe to assume that

Parametric methods are statistical methods that

Exhibit 19-3 It is believed that the median yearly income in a suburb of Atlanta is $70,000. A sample of 67 residents was taken. Thirty-eight had yearly incomes above $70,000, 26 had yearly incomes below $70,000, and 3 had yearly incomes equal to $70,000. The null hypothesis to be tested is H₀: median = $70,000. -Refer to Exhibit 19-3. The p-value for this test is

Two groups of students were asked to rank the activities sponsored by the Student Government Association on campus. The following show their rankings. Determine the Spearman rank-correlation coefficient and test for a significant correlation with $\alpha$ = 0.05.

The monthly sales records of two branches of a department store (Branch A and Branch B) over the last year (12 months) were gathered. It was decided to use the Mann-Whitney-Wilcoxon test to determine if there has been a significant difference between the sales of the two branches. a.Provide the hypotheses for this test. b.Compute the mean $\mu$ _T. c.Compute the standard deviation $\sigma$ _T. d.The sum of the ranks for branch A was determined to be 184.5. Compute the test statistic Z. e.Use $\alpha$ = 0.05 and test to determine if there is a significant difference in the populations of the sales of the two branches.

The level of measurement that allows for the rank ordering of data items is

We want to see if the workers on the day and night shifts differ significantly in their productivity levels. A sample of workers from both shifts was taken. 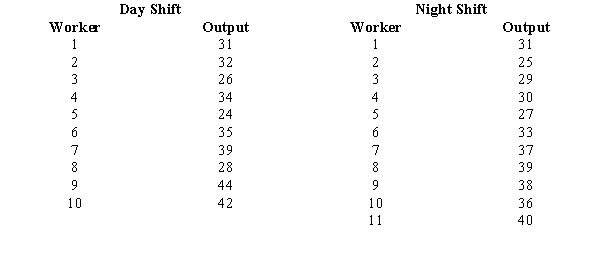a.State the null and alternative hypotheses. b.Test the null hypothesis at the 5% level of significance.

In a questionnaire, respondents are asked to mark their marital status. Marital status is an example of the

Exhibit 19-2 Students in statistics classes were asked whether they preferred a 10-minute break or to get out of class 10 minutes early. In a sample of 150 students, 40 preferred a 10-minute break, 80 preferred to get out 10 minutes early, and 30 had no preference. We want to determine if there is a difference in students' preferences. -Refer to Exhibit 19-2. The test statistic based on the number of students who preferred to get out early equals

Exhibit 19-2 Students in statistics classes were asked whether they preferred a 10-minute break or to get out of class 10 minutes early. In a sample of 150 students, 40 preferred a 10-minute break, 80 preferred to get out 10 minutes early, and 30 had no preference. We want to determine if there is a difference in students' preferences. -Refer to Exhibit 19-2. To test the null hypothesis, the appropriate probability distribution to use is the

A nonparametric method for determining the differences between two populations based on two matched samples where only preference data is required is the

Exhibit 19-6 Forty-one individuals from a sample of 60 indicated they oppose legalized abortion. We are interested in determining whether or not there is a significant difference between the proportions of opponents and proponents of legalized abortion. -Refer to Exhibit 19-6. p-value is

The following data show the preference of 20 people for a candidate to a public office. A "+" indicates a preference for the Democratic candidate, and a "-" indicates a preference for the Republican candidate. With $\alpha$ = 0.05, test for a significant difference in the preference for the candidates.

Exhibit 19-6 Forty-one individuals from a sample of 60 indicated they oppose legalized abortion. We are interested in determining whether or not there is a significant difference between the proportions of opponents and proponents of legalized abortion. -Refer to Exhibit 19-6. The null hypothesis that is being tested is

Exhibit 19-5 It has been hypothesized that there is no difference in the mathematical ability of men and women. To test this hypothesis, it was decided to use the Mann-Whitney-Wilcoxon test. A sample of men and women were given math tests. The scores on the tests are given below. 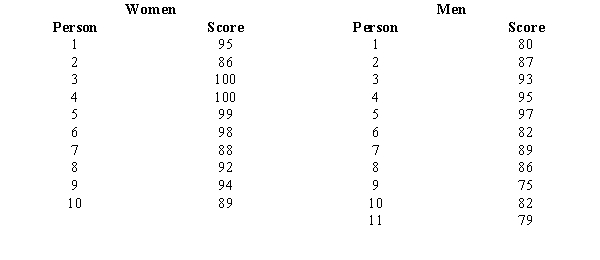-Refer to Exhibit 19-5. The standard deviation ( $\sigma$ _T) is

Fifteen people were asked to indicate their preference for domestic versus imported cars. The following data showed their preferences. 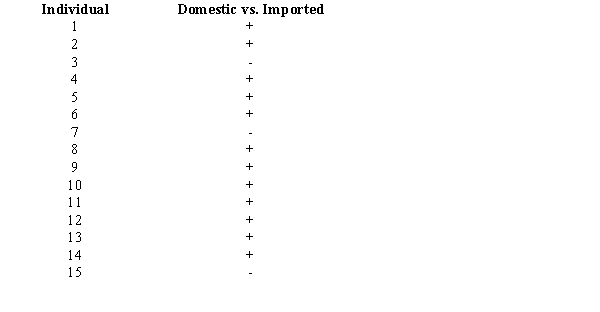With $\alpha$ = 0.05, test for a significant difference in the preferences for cars. A "+" indicates a preference for imported cars.

In a sample of 120 people, 50 indicated that they prefer domestic automobiles, 60 said they prefer foreign-made cars, and 10 indicated no difference in their preference. At a 0.05 level of significance, determine if there is evidence of a significant difference in the preferences for the two makes of automobiles.