Exam 9: Hypothesis Tests
Exam 1: Data and Statistics98 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays62 Questions
Exam 3: Descriptive Statistics: Numerical Measures173 Questions
Exam 4: Introduction to Probability138 Questions
Exam 5: Discrete Probability Distributions123 Questions
Exam 6: Continuous Probability Distributions174 Questions
Exam 7: Sampling and Sampling Distributions133 Questions
Exam 8: Interval Estimation137 Questions
Exam 9: Hypothesis Tests148 Questions
Exam 10: Inference About Means and Proportions With Two Populations121 Questions
Exam 11: Inferences About Population Variances90 Questions
Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit90 Questions
Exam 13: Experimental Design and Analysis of Variance115 Questions
Exam 14: Simple Linear Regression146 Questions
Exam 15: Multiple Regression115 Questions
Exam 16: Regression Analysis: Model Building76 Questions
Exam 17: Time Series Analysis and Forecasting68 Questions
Exam 18: Nonparametric Methods81 Questions
Exam 19: Statistical Methods for Quality Control29 Questions
Exam 20: Index Numbers52 Questions
Exam 21: Decision Analysis on Website65 Questions
Exam 22: Sample Survey on Website63 Questions
Select questions type
If the level of significance of a hypothesis test is raised from .01 to .05, the probability of a Type II error
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
C
The manager of an automobile dealership is considering a new bonus plan in order to increase sales. Currently, the mean sales rate per salesperson is five automobiles per month. The correct set of hypotheses for testing the effect of the bonus plan is
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
B
If a hypothesis is not rejected at the 5% level of significance, it
(Multiple Choice)
4.9/5  (41)
(41)
Some people who bought X-Game gaming systems complained about having received defective systems. The industry standard for such systems has been ninety-eight percent non-defective systems. In a sample of 120 units sold, 6 units were defective.
a.Compute the proportion of defective items in the sample.
b.
b.Compute the standard error of 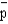 .
c.At 95% confidence using the critical value approach, test to see if the percentage of defective systems produced by X-Game has exceeded the industry standard.
d.Show that the p-value approach results in the same conclusion as that of part
.
c.At 95% confidence using the critical value approach, test to see if the percentage of defective systems produced by X-Game has exceeded the industry standard.
d.Show that the p-value approach results in the same conclusion as that of part
(Essay)
4.9/5  (32)
(32)
The average monthly rent for one-bedroom apartments in Chattanooga has been $700. Because of the downturn in the real estate market, it is believed that there has been a decrease in the average rental. The correct hypotheses to be tested are
(Multiple Choice)
4.7/5  (45)
(45)
The Department of Economic and Community Development (DECD) reported that in 2009 the average number of new jobs created per county was 450. The department also provided the following information regarding a sample of 5 counties in 2010.  a.Compute the sample average and the standard deviation for 2010.
b.We want to determine whether there has been a significant decrease in the average number of jobs created. Provide the null and the alternative hypotheses.
c.Compute the test statistic.
d.Compute the p-value; and at 95% confidence, test the hypotheses. Assume the population is normally distributed.
a.Compute the sample average and the standard deviation for 2010.
b.We want to determine whether there has been a significant decrease in the average number of jobs created. Provide the null and the alternative hypotheses.
c.Compute the test statistic.
d.Compute the p-value; and at 95% confidence, test the hypotheses. Assume the population is normally distributed.
(Essay)
4.8/5  (33)
(33)
The average hourly wage of computer programmers with 2 years of experience has been $21.80. Because of high demand for computer programmers, it is believed there has been a significant increase in the average wage of computer programmers. To test whether or not there has been an increase, the correct hypotheses to be tested are
(Multiple Choice)
4.8/5  (32)
(32)
Consider the following hypothesis test:
Ho: = 10
Ha: 10
A sample of 81 provides a sample mean of 9.5 and a sample standard deviation of 1.8.
a.Determine the standard error of the mean.
b.Compute the value of the test statistic.
c.Determine the p-value; and at 95% confidence, test the above hypotheses.
(Essay)
5.0/5  (43)
(43)
In order to determine the average price of hotel rooms in Atlanta, a sample of 64 hotels was selected. It was determined that the average price of the rooms in the sample was $108.50 with a standard deviation of $16.
a.Formulate the hypotheses to determine whether or not the average room price is significantly different from $112.
b.Compute the test statistic.
c.At 95% confidence using the p-value approach, test the hypotheses. Let = 0.1.
(Essay)
4.8/5  (29)
(29)
In a two-tailed hypothesis test situation, the test statistic is determined to be t = -2.692. The sample size has been 45. The p-value for this test is
(Multiple Choice)
4.8/5  (40)
(40)
Before the last presidential debates, 50% of registered votes indicated they were planning to vote for the incumbent president. In a recent poll of 1200 registered voters after the debates, 636 indicated they are planning to vote for the incumbent president. Has there been a significant increase in the proportion of registered voters who are planning to vote for the incumbent president?
a.State the null and alternative hypotheses to be tested.
b.Compute the test statistic.
c.The null hypothesis is to be tested at 95% confidence. Determine the critical value(s) for this test.
d.What do you conclude?
e.Compute the p-value.
(Essay)
4.9/5  (33)
(33)
Consider the following hypotheses test.
Ho: 80
Ha: < 80
A sample of 121 provided a sample mean of 77.3. The population standard deviation is known to be 16.5.
a.Compute the value of the test statistic.
b.Determine the p-value; and at 93.7% confidence, test the above hypotheses.
c.Using the critical value approach at 93.7% confidence, test the hypotheses.
(Essay)
4.9/5  (30)
(30)
Exhibit 9-3
n = 49  = 54.8
s = 28
H0:
= 54.8
s = 28
H0: 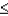 50
Ha: > 50
-Refer to Exhibit 9-3. If the test is done at the 5% level of significance, the null hypothesis should
50
Ha: > 50
-Refer to Exhibit 9-3. If the test is done at the 5% level of significance, the null hypothesis should
(Multiple Choice)
4.8/5  (31)
(31)
You are given the following information obtained from a random sample of 5 observations. Assume the population has a normal distribution.
20 18 17 22 18
You want to determine whether or not the mean of the population from which this sample was taken is significantly less than 21.
a.State the null and the alternative hypotheses.
b.Compute the standard error of the mean.
c.Determine the test statistic.
d.Determine the p-value and at 90% confidence, test whether or not the mean of the population is significantly less than 21.
(Essay)
4.9/5  (36)
(36)
A soft drink filling machine, when in perfect adjustment, fills the bottles with 12 ounces of soft drink. A random sample of 49 bottles is selected, and the contents are measured. The sample yielded a mean content of 11.88 ounces with a standard deviation of 0.35 ounces.
a.Formulate the hypotheses to test to determine if the machine is in perfect adjustment.
b.Compute the value of the test statistic.
c.Compute the p-value and give your conclusion regarding the adjustment of the machine. Let = .05.
(Essay)
4.7/5  (34)
(34)
Exhibit 9-6
A random sample of 16 students selected from the student body of a large university had an average age of 25 years and a standard deviation of 2 years. We want to determine if the average age of all the students at the university is significantly more than 24. Assume the distribution of the population of ages is normal.
-Refer to Exhibit 9-6. The test statistic is
(Multiple Choice)
4.8/5  (39)
(39)
For a one-tailed test (lower tail) with 22 degrees of freedom at 95% confidence, the value of t =
(Multiple Choice)
5.0/5  (36)
(36)
Showing 1 - 20 of 148
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)