Exam 7: Sampling and Sampling Distributions
Exam 1: Data and Statistics98 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays62 Questions
Exam 3: Descriptive Statistics: Numerical Measures173 Questions
Exam 4: Introduction to Probability138 Questions
Exam 5: Discrete Probability Distributions123 Questions
Exam 6: Continuous Probability Distributions174 Questions
Exam 7: Sampling and Sampling Distributions133 Questions
Exam 8: Interval Estimation137 Questions
Exam 9: Hypothesis Tests148 Questions
Exam 10: Inference About Means and Proportions With Two Populations121 Questions
Exam 11: Inferences About Population Variances90 Questions
Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit90 Questions
Exam 13: Experimental Design and Analysis of Variance115 Questions
Exam 14: Simple Linear Regression146 Questions
Exam 15: Multiple Regression115 Questions
Exam 16: Regression Analysis: Model Building76 Questions
Exam 17: Time Series Analysis and Forecasting68 Questions
Exam 18: Nonparametric Methods81 Questions
Exam 19: Statistical Methods for Quality Control29 Questions
Exam 20: Index Numbers52 Questions
Exam 21: Decision Analysis on Website65 Questions
Exam 22: Sample Survey on Website63 Questions
Select questions type
A sample of 92 observations is taken from an infinite population. The sampling distribution of  is approximately
is approximately
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
C
Below you are given the values obtained from a random sample of 4 observations taken from an infinite population. 32 34 35 39
a.Find a point estimate for . Is this an unbiased estimate of ? Explain.
b.Find a point estimate for 2. Is this an unbiased estimate of 2? Explain.
c.Find a point estimate for .
d.What can be said about the sampling distribution of  ? Be sure to discuss the expected value, the standard deviation, and the shape of the sampling distribution of
? Be sure to discuss the expected value, the standard deviation, and the shape of the sampling distribution of  .
.
Free
(Essay)
4.9/5  (50)
(50)
Correct Answer:
a.35; Yes; E(x) =
b.8.667; Yes; E(s2) = 2
c.2.944
d.E(  ) = , the standard deviation = 2/n, and the sampling distribution of
) = , the standard deviation = 2/n, and the sampling distribution of  is normally distributed if the population is normally distributed.
is normally distributed if the population is normally distributed.
Which of the following is(are) point estimator(s)?
Free
(Multiple Choice)
4.8/5  (28)
(28)
Correct Answer:
C
A sample of 66 observations will be taken from an infinite population. The population proportion equals 0.12. The probability that the sample proportion will be less than 0.1768 is
(Multiple Choice)
4.9/5  (38)
(38)
Random samples of size 100 are taken from an infinite population whose population proportion is 0.2. The mean and standard deviation of the sample proportion are
(Multiple Choice)
4.8/5  (38)
(38)
Michael is running for president. The proportion of voters who favor Michael is 0.8. A simple random sample of 100 voters is taken.
a.What are the expected value, standard deviation, and shape of the sampling distribution of 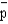 ?
b.What is the probability that the number of voters in the sample who will not favor Michael will be between 26 and 30?
c.What is the probability that the number of voters in the sample who will not favor Michael will be more than 16?
?
b.What is the probability that the number of voters in the sample who will not favor Michael will be between 26 and 30?
c.What is the probability that the number of voters in the sample who will not favor Michael will be more than 16?
(Short Answer)
4.7/5  (37)
(37)
A population characteristic, such as a population mean, is called
(Multiple Choice)
4.8/5  (41)
(41)
In a restaurant, the proportion of people who order coffee with their dinner is .9. A simple random sample of 144 patrons of the restaurant is taken.
a.What are the expected value, standard deviation, and shape of the sampling distribution of 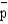 ?
b.What is the probability that the proportion of people who will order coffee with their meal is between 0.85 and 0.875?
c.What is the probability that the proportion of people who will order coffee with their meal is at least 0.945?
?
b.What is the probability that the proportion of people who will order coffee with their meal is between 0.85 and 0.875?
c.What is the probability that the proportion of people who will order coffee with their meal is at least 0.945?
(Short Answer)
5.0/5  (37)
(37)
A department store has determined that 25% of all their sales are credit sales. A random sample of 75 sales is selected.
a.What is the probability that the sample proportion will be greater than 0.34?
b.What is the probability that the sample proportion will be between 0.196 and 0.354?
c.What is the probability that the sample proportion will be less than 0.25?
d.What is the probability that the sample proportion will be less than 0.10?
(Short Answer)
4.8/5  (26)
(26)
Ten percent of the items produced by a machine are defective. A random sample of 100 items is selected and checked for defects.
a.Determine the standard error of the proportion.
b.What is the probability that the sample will contain more than 2.5% defective units?
c.What is the probability that the sample will contain more than 13% defective units?
(Short Answer)
4.9/5  (34)
(34)
Consider a population of five weights identical in appearance but weighing 1, 3, 5, 7, and 9 ounces.
a.Determine the mean and the variance of the population.
b.Sampling without replacement from the above population with a sample size of 2 produces ten possible samples. Using the ten sample mean values, determine the mean of the population and the variance of  .
c.Compute the standard error of the mean.
.
c.Compute the standard error of the mean.
(Short Answer)
4.8/5  (37)
(37)
An automotive repair shop has determined that the average service time on an automobile is 130 minutes with a standard deviation of 26 minutes. A random sample of 40 automotive services is selected.
a.Compute the standard error of the mean.
b.What is the probability that the sample of 40 automotive services will have a mean service time greater than 136 minutes?
c.Assume the population consists of 400 automotive services. Determine the standard error of the mean.
(Short Answer)
4.8/5  (25)
(25)
A population consists of 500 elements. We want to draw a simple random sample of 50 elements from this population. On the first selection, the probability of an element being selected is
(Multiple Choice)
4.9/5  (38)
(38)
Exhibit 7-1
A random sample of 121 bottles of cologne showed an average content of 4 ounces. It is known that the standard deviation of the contents (i.e., of the population) is 0.22 ounces.
-Refer to Exhibit 7-1. In this problem the 0.22 is
(Multiple Choice)
4.7/5  (41)
(41)
A simple random sample of 28 observations was taken from a large population. The sample mean equaled 50. Fifty is a
(Multiple Choice)
4.9/5  (38)
(38)
The following information was collected from a simple random sample of a population. 16
19 18 17 20 18
The point estimate of the mean of the population is
(Multiple Choice)
4.8/5  (35)
(35)
A sample of 400 observations will be taken from an infinite population. The population proportion equals 0.8. The probability that the sample proportion will be greater than 0.83 is
(Multiple Choice)
4.8/5  (40)
(40)
The average lifetime of a light bulb is 3,000 hours with a standard deviation of 696 hours. A simple random sample of 36 bulbs is taken.
a.What are the expected value, standard deviation, and shape of the sampling distribution of  ?
b.What is the probability that the average life in the sample will be between 2,670.56 and 2,809.76 hours?
c.What is the probability that the average life in the sample will be greater than 3,219.24 hours?
d.What is the probability that the average life in the sample will be less than 3,180.96 hours?
?
b.What is the probability that the average life in the sample will be between 2,670.56 and 2,809.76 hours?
c.What is the probability that the average life in the sample will be greater than 3,219.24 hours?
d.What is the probability that the average life in the sample will be less than 3,180.96 hours?
(Essay)
4.9/5  (26)
(26)
A simple random sample of 144 observations was taken from a large population. The sample mean and the standard deviation were determined to be 1234 and 120 respectively. The standard error of the mean is
(Multiple Choice)
4.7/5  (32)
(32)
The standard deviation of all possible  values is called the
values is called the
(Multiple Choice)
4.8/5  (27)
(27)
Showing 1 - 20 of 133
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)