Exam 16: Regression Analysis: Model Building
Exam 1: Data and Statistics98 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays62 Questions
Exam 3: Descriptive Statistics: Numerical Measures173 Questions
Exam 4: Introduction to Probability138 Questions
Exam 5: Discrete Probability Distributions123 Questions
Exam 6: Continuous Probability Distributions174 Questions
Exam 7: Sampling and Sampling Distributions133 Questions
Exam 8: Interval Estimation137 Questions
Exam 9: Hypothesis Tests148 Questions
Exam 10: Inference About Means and Proportions With Two Populations121 Questions
Exam 11: Inferences About Population Variances90 Questions
Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit90 Questions
Exam 13: Experimental Design and Analysis of Variance115 Questions
Exam 14: Simple Linear Regression146 Questions
Exam 15: Multiple Regression115 Questions
Exam 16: Regression Analysis: Model Building76 Questions
Exam 17: Time Series Analysis and Forecasting68 Questions
Exam 18: Nonparametric Methods81 Questions
Exam 19: Statistical Methods for Quality Control29 Questions
Exam 20: Index Numbers52 Questions
Exam 21: Decision Analysis on Website65 Questions
Exam 22: Sample Survey on Website63 Questions
Select questions type
In multiple regression analysis, the word linear in the term "general linear model" refers to the fact that
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
B
What value of Durbin-Watson statistic indicates no autocorrelation is present?
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
B
Multiple regression analysis was used to study the relationship between a dependent variable, Y, and four independent variables; X1, X2, X3 and, X4. The following is a partial result of the regression analysis involving 31 observations. 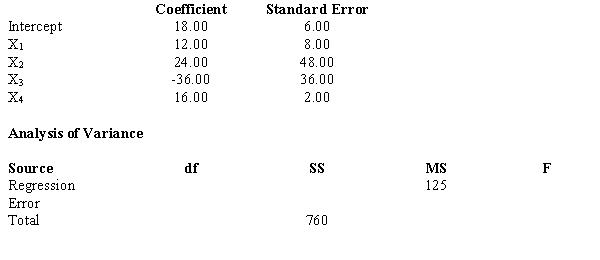 a.Compute the coefficient of determination.
b.Perform a t test and determine whether or not 1 is significantly different from zero ( = 0.05).
c.Perform a t test and determine whether or not 4is significantly different from zero ( = 0.05).
d.At = 0.05, perform an F test and determine whether or not the regression model is significant.
a.Compute the coefficient of determination.
b.Perform a t test and determine whether or not 1 is significantly different from zero ( = 0.05).
c.Perform a t test and determine whether or not 4is significantly different from zero ( = 0.05).
d.At = 0.05, perform an F test and determine whether or not the regression model is significant.
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
a.0.6579
b.t = 1.5; p-value is between 0.1 and 0.2; do not reject H0; not significant (critical t = 2.056)
c.t = 8; p-value < .01; reject H0; significant (critical t = 2.056)
d.F = 12.5; p-value < .01; reject H0; significant (critical F = 2.76)
When dealing with the problem of non-constant variance, the reciprocal transformation means using
(Multiple Choice)
4.9/5  (36)
(36)
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (Y in months) of 33 rats, units of daily protein intake (X1), and whether or not agent X2 (a proposed life extending agent) was added to the rats diet (X2 = 0 if agent X2 was not added, and X2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed. 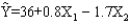 Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The model
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The model
(Multiple Choice)
4.8/5  (37)
(37)
A regression analysis was applied in order to determine the relationship between a dependent variable and 4 independent variables. The following information was obtained from the regression analysis.
R Square = 0.60
SSR = 4,800
Total number of observations n = 35 
(Essay)
4.9/5  (36)
(36)
Part of an Excel output relating Y (dependent variable) and 4 independent variables, X1 through X4, is shown below. 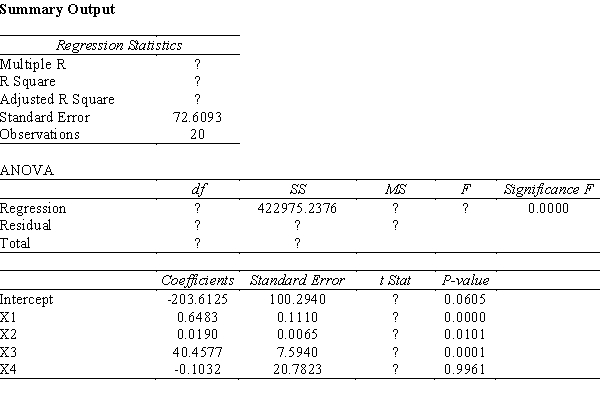 a.Fill in all the blanks marked with "?"
b.At 95% confidence, which independent variables are significant and which ones are not? Fully explain how you arrived at your answers.
a.Fill in all the blanks marked with "?"
b.At 95% confidence, which independent variables are significant and which ones are not? Fully explain how you arrived at your answers.
(Essay)
4.9/5  (35)
(35)
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed. 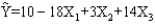 Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4,800
SSE = 1,296
-Refer to Exhibit 16-1. If you want to determine whether or not the coefficients of the independent variables are significant, the critical value of t statistic at = 0.05 is
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4,800
SSE = 1,296
-Refer to Exhibit 16-1. If you want to determine whether or not the coefficients of the independent variables are significant, the critical value of t statistic at = 0.05 is
(Multiple Choice)
4.8/5  (34)
(34)
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (Y in months) of 33 rats, units of daily protein intake (X1), and whether or not agent X2 (a proposed life extending agent) was added to the rats diet (X2 = 0 if agent X2 was not added, and X2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed. 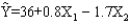 Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The degrees of freedom associated with SSR are
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The degrees of freedom associated with SSR are
(Multiple Choice)
4.9/5  (28)
(28)
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained. 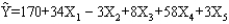 For this model, SSR = 1,740 and SST = 2,000.
-Refer to Exhibit 16-2. The degrees of freedom associated with SSR are
For this model, SSR = 1,740 and SST = 2,000.
-Refer to Exhibit 16-2. The degrees of freedom associated with SSR are
(Multiple Choice)
4.8/5  (34)
(34)
We want to test whether or not the addition of 3 variables to a model will be statistically significant. You are given the following information based on a sample of 25 observations. 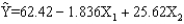 SSE = 725
SSR = 526
The equation was also estimated including the 3 variables. The results are
SSE = 725
SSR = 526
The equation was also estimated including the 3 variables. The results are 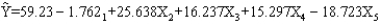 SSE = 520
SSR = 731
a.State the null and alternative hypotheses.
b.Test the null hypothesis at the 5% level of significance.
SSE = 520
SSR = 731
a.State the null and alternative hypotheses.
b.Test the null hypothesis at the 5% level of significance.
(Essay)
4.8/5  (39)
(39)
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (Y in months) of 33 rats, units of daily protein intake (X1), and whether or not agent X2 (a proposed life extending agent) was added to the rats diet (X2 = 0 if agent X2 was not added, and X2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed. 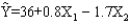 Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The life expectancy of a rat that was not given any protein and that did not take agent X2 is
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The life expectancy of a rat that was not given any protein and that did not take agent X2 is
(Multiple Choice)
4.9/5  (36)
(36)
A variable such as Z, whose value is Z = X1X2 is added to a general linear model in order to account for potential effects of two variables X1 and X2 acting together. This type of effect is
(Multiple Choice)
4.7/5  (39)
(39)
A regression model relating units sold (Y), price (X1), and whether or not promotion was used (X2 = 1 if promotion was used and 0 if it was not) resulted in the following model. 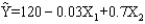 and the following information is provided.
and the following information is provided.  a.Is price a significant variable?
b.Is promotion significant?
a.Is price a significant variable?
b.Is promotion significant?
(Essay)
4.7/5  (39)
(39)
A test to determine whether or not first-order autocorrelation is present is
(Multiple Choice)
4.7/5  (35)
(35)
Ziba, Inc. has provided the following information regarding their sales for January through December of 2009. (Part of the data file is shown below.)  The results of the regression analysis relating these variables are shown below.
The results of the regression analysis relating these variables are shown below.  a.The company is planning to increase their advertising by 5% per month for the months of January and February of 2010. What would be the advertising for January and February of 2010? Give your answers in dollars.
b.Use the regression model that is provided above and forecast sales for January and February of 2010, assuming the company increases their advertising by 5% per month for the months of January and February of 2010. Show your computations and write your answers in dollars below.
a.The company is planning to increase their advertising by 5% per month for the months of January and February of 2010. What would be the advertising for January and February of 2010? Give your answers in dollars.
b.Use the regression model that is provided above and forecast sales for January and February of 2010, assuming the company increases their advertising by 5% per month for the months of January and February of 2010. Show your computations and write your answers in dollars below.
(Essay)
4.7/5  (36)
(36)
A regression model with one independent variable, X1, resulted in an SSE of 50. When a second independent variable, X2, was added to the model, the SSE was reduced to 40. At = 0.05, determine if X2 contributes significantly to the model. The sample size for both models was 30.
(Essay)
4.9/5  (37)
(37)
A regression analysis (involving 45 observations) relating a dependent variable (Y) and two independent variables resulted in the following information. 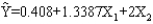 The SSE for the above model is 49.
When two other independent variables were added to the model, the following information was provided.
The SSE for the above model is 49.
When two other independent variables were added to the model, the following information was provided. 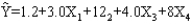 This latter model's SSE is 40.
At 95% confidence test to determine if the two added independent variables contribute significantly to the model.
This latter model's SSE is 40.
At 95% confidence test to determine if the two added independent variables contribute significantly to the model.
(Essay)
4.8/5  (33)
(33)
Showing 1 - 20 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)