Exam 4: Introduction to Probability

A survey of a sample of business students resulted in the following information regarding the genders of the individuals and their selected major. Selected Major 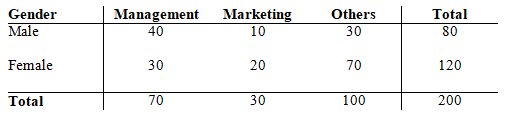a.What is the probability of selecting an individual who is majoring in Marketing? b.What is the probability of selecting an individual who is majoring in Management, given that the person is female? c.Given that a person is male, what is the probability that he is majoring in Management? d.What is the probability of selecting a male individual?

The sample space refers to

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

You are applying for graduate school at University A. In the past 42% of the applicants to this university have been accepted. It is also known that 70% of those students who have been accepted have had GMAT scores in excess of 550 while 40% of the students who were not accepted had GMAT scores in excess of 550. You take the GMAT exam and score 640. What is the probability that you will be accepted into graduate school of university A?

Tammy is a general contractor and has submitted two bids for two projects (A and B). The probability of getting project A is 0.65. The probability of getting project B is 0.77. The probability of getting at least one of the projects is 0.90. a.What is the probability that she will get both projects? b.Are the events of getting the two projects mutually exclusive? Explain, using probabilities. c.Are the two events independent? Explain, using probabilities.

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

If P(A) = 0.62, P(B) = 0.47, and P(A $\cup$ B) = 0.88, then P(A $\cap$ B) =

Assume you have applied for two scholarships, a Merit scholarship (M) and an Athletic scholarship (A). The probability that you receive an Athletic scholarship is 0.18. The probability of receiving both scholarships is 0.11. The probability of getting at least one of the scholarships is 0.3. a.What is the probability that you will receive a Merit scholarship? b.Are events A and M mutually exclusive? Why or why not? Explain. c.Are the two events A, and M, independent? Explain, using probabilities. d.What is the probability of receiving the Athletic scholarship given that you have been awarded the Merit scholarship? e.What is the probability of receiving the Merit scholarship given that you have been awarded the Athletic scholarship?

If A and B are mutually exclusive events with P(A) = 0.3 and P(B) = 0.5, then P(A $\cup$ B) =

An automobile dealer has kept records on the customers who visited his showroom. Forty percent of the people who visited his dealership were female. Furthermore, his records show that 35% of the females who visited his dealership purchased an automobile, while 20% of the males who visited his dealership purchased an automobile. Let A₁ = the event that the customer is female A₂ = the event that the customer is male a.What is the probability that a customer entering the showroom will buy an automobile? b.A car salesperson has just informed us that he sold a car to a customer. What is the probability that the customer was female?

Since the sun must rise tomorrow, then the probability of the sun rising tomorrow is

If A and B are independent events with P(A) = 0.05 and P(B) = 0.65, then P(A | B) =

The symbol $\cap$ shows the

A student has to take 9 more courses before he can graduate. If none of the courses are prerequisite to others, how many groups of four courses can he select for the next semester?

If A and B are independent events with P(A) = 0.38 and P(B) = 0.55, then P(A | B) =

In a horse race, nine horses are running. Assume you have purchased a Trifecta ticket. (In Trifecta, the player selects three horses as first, second, and third place winners. To win, those three horses must finish the race in the precise order the player has selected.) How many possibilities of a Trifecta exist?

Assume your favorite soccer team has 3 games left to finish the season. The outcome of each game can be win, lose, or tie. How many possible outcomes exist?

Events that have no sample points in common are