Exam 18: Simple Linear Regression and Correlation

The confidence interval estimate of the expected value of y will be narrower than the prediction interval for the same given value of x and confidence level. This is because there is less error in estimating a mean value than in predicting an individual value.

Given that the sum of squares for error is 50 and the sum of squares for regression is 140, the coefficient of determination is:

In a regression problem the following pairs (x, y) are given: (3,-2), (3,-1), (3,0), (3,1) and (3,2). This indicates that the coefficient of correlation is -1.

Which of the following techniques is used to predict the value of one variable on the basis of other variables?

A financier whose specialty is investing in movie productions has observed that, in general, movies with 'big-name' stars seem to generate more revenue than those movies whose stars are less well known. To examine his belief, he records the gross revenue and the payment (in $ million) given to the two highest-paid performers in the movie for 10 recently released movies. Movie Cost of two highest- paid performers (\ ) Gross revenue (\ ) 1 5.3 48 2 7.2 65 3 1.3 18 4 1.8 20 5 3.5 31 6 2.6 26 7 8.0 73 8 2.4 23 9 4.5 39 10 6.7 58 Compute the standardised residuals.

Which of the following best describes the coefficient of determination?

A financier whose specialty is investing in movie productions has observed that, in general, movies with 'big-name' stars seem to generate more revenue than those movies whose stars are less well known. To examine his belief, he records the gross revenue and the payment (in $ million) given to the two highest-paid performers in the movie for 10 recently released movies. Conduct a test of the population coefficient of correlation to determine at the 5% significance level whether a linear relationship exists between payment to the two highest-paid performers and gross revenue.

The quality of oil is measured in API gravity degrees - the higher the degrees API, the higher the quality. The table shown below is produced by an expert in the field, who believes that there is a relationship between quality and price per barrel. Oil degrees API Price per barrel (in \ ) 27.0 12.02 28.5 12.04 30.8 12.32 31.3 12.27 31.9 12.49 34.5 12.70 34.0 12.80 34.7 13.00 37.0 13.00 41.0 13.17 41.0 13.19 38.8 13.22 39.3 13.27 A partial Minitab output follows. Descriptive Statistics Variable Mean StDev SE Mean Degrees 13 34.60 4.613 1.280 Frice 13 12.730 0.457 0.127 Covariances Degrees Price Degrees 21.281667 Price 2.026750 0.208833 Regression Analysis Predictor Coef StDev Constant 9.4349 0.2867 32.91 0.000 Degrees 0.095235 0.008220 11.59 0.000 S = 0.1314 R-Sq = 92.46% R-Sq(adj) = 91.7% Analysis of Variance Source DF SS MS F P Regression 1 2.3162 2.3162 134.24 0.000 Residual Error 11 0.1898 0.0173 Total 12 2.5060 a. Draw a scatter diagram of the data to determine whether a linear model appears to be appropriate to describe the relationship between the quality of oil and price per barrel. b. Determine the least squares regression line. c. Redraw the scatter diagram and plot the least squares regression line on it. d. Interpret the value of the slope of the regression line.

A professor of economics wants to study the relationship between income y (in $1000s) and education x (in years). A random sample of eight individuals is taken and the results are shown below. Education 16 11 15 8 12 10 13 14 Income 58 40 55 35 43 41 52 49 Interpret the value of the slope of the regression line.

An economist wanted to analyse the relationship between the speed of a car (x) in kilometres per hour (kmph) and its fuel consumption (y) in kilometres per litre (kmpl). In an experiment, a car was operated at several different speeds and for each speed the fuel consumption was measured. The data obtained are shown below. Speed (mph) 25 35 45 50 60 65 70 Fuel consumtion (mpg) 40 39 37 33 30 27 25 a. Find the least squares regression line. b. Calculate the standard error of estimate, and describe what this statistic tells you about the regression line. c. Do these data provide sufficient evidence at the 5% significance level to infer that a linear relationship exists between higher speeds and lower fuel consumption? d. Predict with 99% confidence the fuel consumption of a car traveling at 55 kmph.

Statisticians have shown that the sample y-intercept $b _ { 0 }$ and sample slope coefficient $b _ { 1 }$ are unbiased estimators of the population regression parameters $\beta _ { 0 }$ and $\beta _ { 1 }$ .

In order to estimate with 95% confidence the expected value of y in a simple linear regression problem, a random sample of 10 observations is taken. Which of the following t-table values listed below would be used?

A simple linear regression equation is given by 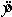$= 5.25 + 3.8 x$ . The point estimate of $y$ when $x$ = 4 is 20.45.

A professor of economics wants to study the relationship between income y (in $1000s) and education x (in years). A random sample of eight individuals is taken and the results are shown below. Education 16 11 15 8 12 10 13 14 Income 58 40 55 35 43 41 52 49 Use the predicted and actual values of y to calculate the residuals.

Given the following linear regression model of Weekly sales ($000's) in a fast food restaurant against number of vouchers printed in the local newspaper, interpret the intercept. Does this make sense? Estimated Sales = 11.5676 + 0.4618.Vouchers

An ardent fan of television game shows has observed that, in general, the more educated the contestant, the less money he or she wins. To test her belief, she gathers data about the last eight winners of her favourite game show. She records their winnings in dollars and their years of education. The results are as follows. Contestant Years of education Winnings 1 11 750 2 15 400 3 12 600 4 16 350 5 11 800 6 16 300 7 13 650 8 14 400 Compute the standardised residuals.

The variance of the error variable, $\sigma _ { \varepsilon } ^ { 2 }$ , is required to be constant. When this requirement is satisfied, the condition is called homoscedasticity.

An ardent fan of television game shows has observed that, in general, the more educated the contestant, the less money he or she wins. To test her belief, she gathers data about the last eight winners of her favourite game show. She records their winnings in dollars and their years of education. The results are as follows. Contestant Years of education Winnings 1 11 750 2 15 400 3 12 600 4 16 350 5 11 800 6 16 300 7 13 650 8 14 400 Identify possible outliers.

A scatter diagram includes the following data points: x 3 2 5 4 5 y 9 6 11 11 15 Two regression models are proposed: Model 1: y-hat = 1.85 + 2.40x. Model 2: y-hat = 1.79 + 2.54x. Using the least squares method, which of these regression models provides the better fit to the data? Why?

Which of the following best describes if we want to test for a linear relationship between x and y, in regression analysis?