Exam 4: Describing Bivariate Numerical Data
Exam 1: Collecting Data in Reasonable Ways56 Questions
Exam 2: Graphical Methods for Describing Data Distributions62 Questions
Exam 3: Numerical Methods for Describing Data Distributions37 Questions
Exam 4: Describing Bivariate Numerical Data70 Questions
Exam 5: Probability55 Questions
Exam 6: Random Variables and Probability Distributions72 Questions
Exam 7: An Overview of Statistical Inference - Learning From Data19 Questions
Exam 8: Sampling Variability and Sampling Distributions35 Questions
Exam 9: Estimating a Population Proportion36 Questions
Exam 10: Asking and Answering Questions About a Population Proportion31 Questions
Exam 11: Asking and Answering Questions About the Difference Between Two Proportions42 Questions
Exam 12: Asking and Answering Questions About a Population Mean51 Questions
Exam 13: Asking and Answering Questions About the Difference Between Two Means46 Questions
Exam 14: Learning From Categorical Data36 Questions
Exam 15: Understanding Relationships - Numerical Data Part 243 Questions
Exam 16: Asking and Answering Questions About More Than Two Means25 Questions
Select questions type
Exhibit 4-4:
Biological theory suggests that the relationship between the weight of these animals and their wing length is exponential, i.e. W = α(10)βL, or W = α(e)βL where W is the wing weight and L is the wing length. 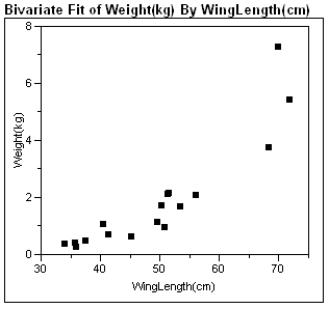 -Refer to Exhibit 4-4.
For a wing length of the data point where L = 56.0 (Hieraeus fasciatus), what is the predicted bird weight? Show your work below.
-Refer to Exhibit 4-4.
For a wing length of the data point where L = 56.0 (Hieraeus fasciatus), what is the predicted bird weight? Show your work below.
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
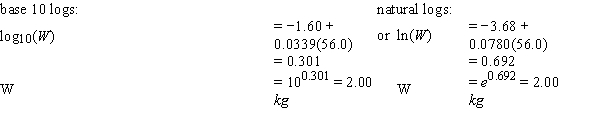
If on average y increases as x increases, the correlation coefficient is positive.
Free
(True/False)
4.8/5  (26)
(26)
Correct Answer:
True
Exhibit 4-1
The preservation of objects made of organic material is a constant concern to those caring for items of historical interest. For example, some delicate fabrics are natural silks--they are made of protein and are biodegradable. Many silks in museum collections are in danger of crumbling. It would be of great benefit to be able to assess the delicacy of the fabric before making decisions about displaying it. One possibility is chemical analysis, which might give some evidence about the brittle nature of a fabric. To investigate this possibility, bio-chemical data in the form of a ratio of the amount of certain amino acids in the fibers was acquired from the linings of sixteen 19th and early 20th century Japanese kimonos, and the tenacity (breaking stress) of the fabric was also recorded.
Using the data from the Japanese kimonos, construct the least squares best fit line predicting tenacity using amino acid ratio as a predictor. 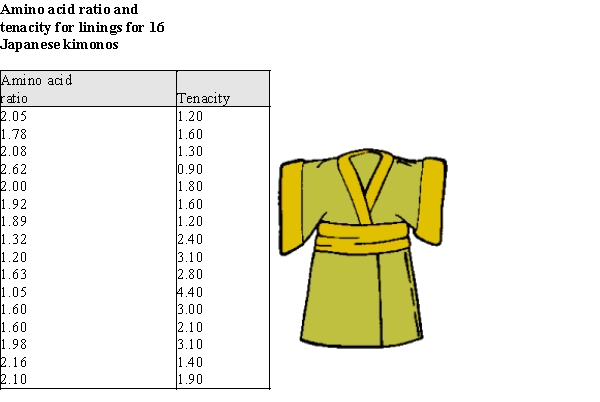 -Refer to Exhibit 4-1.
Approximately what proportion of the variability in tenacity is explained by the amino acid ratio?
-Refer to Exhibit 4-1.
Approximately what proportion of the variability in tenacity is explained by the amino acid ratio?
Free
(Short Answer)
4.8/5  (29)
(29)
Correct Answer:
r2 = .636.
Data on x = the weight of a pickup truck (pounds) and y = distance (in feet) required for a truck traveling 40 miles per hour to come to a complete stop for 30 trucks was used to fit the least squares regression line 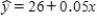 . Which of the following statements is a correct interpretation of the value 0.05 in the equation of the regression line?
. Which of the following statements is a correct interpretation of the value 0.05 in the equation of the regression line?
(Multiple Choice)
4.8/5  (41)
(41)
Exhibit 4-3
Paleontology, the study of forms of prehistoric life, can sometimes be aided by modern biology. The study of prehistoric birds depends on fossil information, which typically consists of imprints in stone of a prehistoric creature's remains. To study the productivity of an ancient ecosystem it would be useful know the actual mass of the individual birds, but this information is not preserved in the fossil record. It seems reasonable that the biomechanics of birds operates much the same today as in the past. For example, relationship between the wing length and total weight of a bird should be very similar today to the relationship in the distant past. The wing lengths of ancient birds are readily obtainable from the fossil record, but the weight is not. Assuming similar biomechanical development for ancient birds and modern birds, a regression model expressing the relationship between wing length and total weight of a modern bird could be used to estimate the mass of similar prehistoric birds and thus gauge some aspects of the ancient ecosystem.
Data is available for some modern birds of prey. Specifically, data on the mean wing length and mean total weight of species of hawk-like birds of prey is given below. 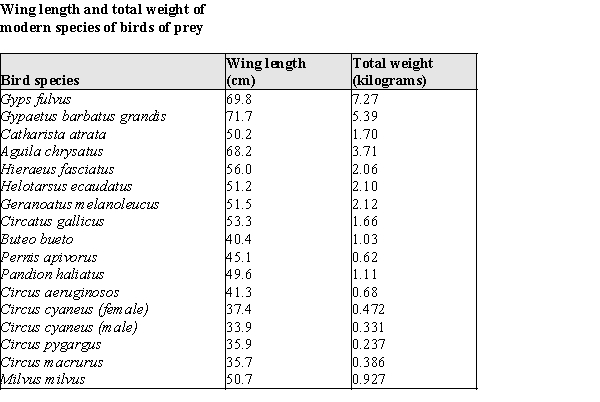 -Refer to Exhibit 4-3. Approximately what proportion of the variability in weight is explained by the wing length?
-Refer to Exhibit 4-3. Approximately what proportion of the variability in weight is explained by the wing length?
(Essay)
4.8/5  (30)
(30)
In the season 2016-2017 Chelsea won English Premier League. Ron and Tom, fans of Chelsea, argued which factor was more important for winning the League: the number of goals scored or the number of goals conceded. Using the information about the results of the season 2016-2017 represented in the table below ( http://www.espn.com/soccer/standings/_/league/eng.1/season/2016/sort/points), find out, which factor has been statistically more important. 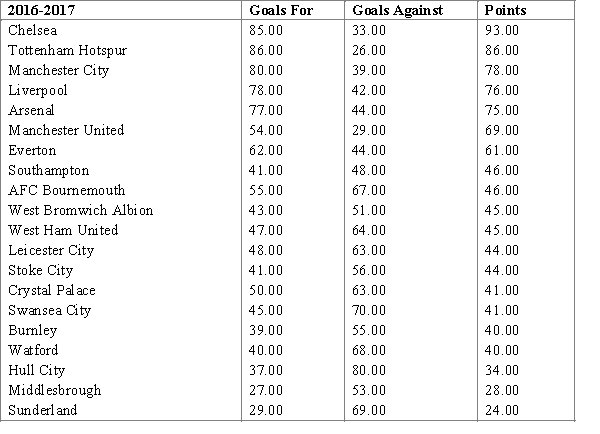
(Multiple Choice)
4.7/5  (30)
(30)
The Des Moines Register recently reported the ratings of high school sportsmanship as compiled by the Iowa High School Athletic Association. For each school the participants and coaches were rated by referees, where 1 = superior, and 5 = unsatisfactory. A regression analysis of the average scores given to football players and coaches is shown below. 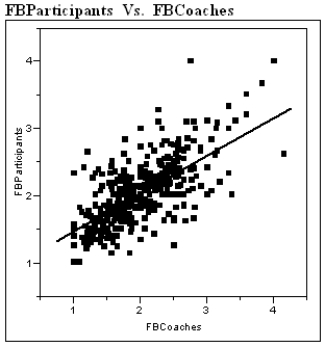 Linear Fit
FBParticipants = 0.902 + 0.568 FBCoaches
Linear Fit
FBParticipants = 0.902 + 0.568 FBCoaches 

a)Interpret the value of the correlation between the ratings of coaches and participants.
b)Interpret the value of the coefficient of determination.
c)Interpret the value of the standard deviation about the least squares line.
a)Interpret the value of the correlation between the ratings of coaches and participants.
b)Interpret the value of the coefficient of determination.
c)Interpret the value of the standard deviation about the least squares line.
(Essay)
4.8/5  (42)
(42)
Consider the following five scatterplots. All are drawn to the same scale on both the x and y axes. For which scatterplot is the relationship negative?
(Multiple Choice)
4.8/5  (24)
(24)
The data below were gathered on a random sample of 7 male black-footed albatrosses of known age. In an effort to monitor diseases of these animals, biologists would like to be able to estimate the age of animals that have died by flattening their gonads and measuring the resulting area. 
a)What is the value of the correlation coefficient for these data?
b)What is the equation of the least squares line describing the relationship between x = Gonad Size and y = Age.
c)If these albatrosses are representative of the population, what would you predict to be the age of a male albatross with a gonad size of 50 sq. mm? Show any calculations below.
d)The largest albatross gonad size in the sample was 96 sq mm, with an age of 23.64 years. These animals are thought to live for up to 40 years. Would it be reasonable to use the equation from part (b) above to predict the age for a gonad size of 150 sq mm? Why or why not?
a)What is the value of the correlation coefficient for these data?
b)What is the equation of the least squares line describing the relationship between x = Gonad Size and y = Age.
c)If these albatrosses are representative of the population, what would you predict to be the age of a male albatross with a gonad size of 50 sq. mm? Show any calculations below.
d)The largest albatross gonad size in the sample was 96 sq mm, with an age of 23.64 years. These animals are thought to live for up to 40 years. Would it be reasonable to use the equation from part (b) above to predict the age for a gonad size of 150 sq mm? Why or why not?
(Essay)
4.8/5  (38)
(38)
Assessing the goodness of fit of a regression line involves considering several things, and no single characteristic of data is sufficient for a good assessment. Consider the characteristics below. How does each contribute to an assessment of fit? That is, for each piece of information, what about it would indicate a "good" best-fit line?
a)The shape of the residual plot
b)The correlation coefficient
c)The demonstration of seriously influential points
d)The coefficient of determination
(Essay)
4.8/5  (28)
(28)
Exhibit 4-2
The theory of fiber strength suggests that the relationship between fiber tenacity and amino acid ratio is logarithmic, i.e. 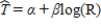 , where T is the tenacity and R is the amino acid ratio.
Perform the appropriate transformation of variable(s) and fit this logarithmic model to the data.
, where T is the tenacity and R is the amino acid ratio.
Perform the appropriate transformation of variable(s) and fit this logarithmic model to the data.
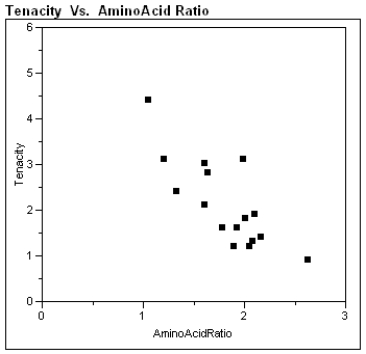 -Refer to Exhibit 4-2. Does it appear that the transformed model is no improvement over the linear model, a slight improvement, or a significant improvement? Justify your response with an appropriate statistical argument.
-Refer to Exhibit 4-2. Does it appear that the transformed model is no improvement over the linear model, a slight improvement, or a significant improvement? Justify your response with an appropriate statistical argument.
(Essay)
4.9/5  (28)
(28)
In the 19th Century, venereal diseases were the major preventable diseases striking soldiers far from home. During the American Civil War, the United States Army kept records on soldiers diagnosed with syphilis and gonorrhea. An analysis of the incidence of these diseases is presented below. (Incidence is the rate of increase in the number of cases--for these data, the incidence is number of soldiers per 100,000 per month.) 
r = 0.914,
r = 0.914, 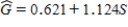 a)If, at a particular point in time, the incidence rate for Syphilis is one standard deviation above the mean, what would be the predicted incidence rate for gonorrhea?
a)If, at a particular point in time, the incidence rate for Syphilis is one standard deviation above the mean, what would be the predicted incidence rate for gonorrhea?
(Essay)
4.9/5  (31)
(31)
If a scatter plot exhibits a strong negative relationship, what can be said about the value of the quantity,  ?
?
(Short Answer)
4.9/5  (39)
(39)
The use of small aircraft with human observers is common in wildlife studies where the goal is to estimate the abundance of different species. Recently there has been interest in using unmanned aerial vehicles (UAV). The UAV, something about the size of a model airplane, would fly over the area of interest and take pictures to be analyzed by computers with imagery software when the UAV returns. The plot below is from a test run of the UAV over 10 areas in South Central Florida, using bird decoys to test the reliability of the process. 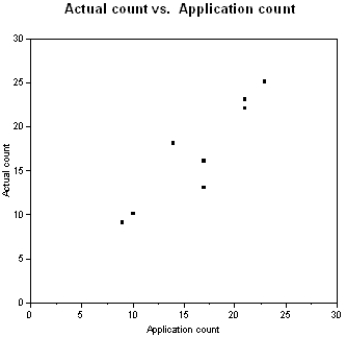 (a)The least squares best fit line is
(a)The least squares best fit line is 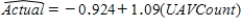 . Plot this line on the graph above. Show any calculations in the space below.
(b)The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.
. Plot this line on the graph above. Show any calculations in the space below.
(b)The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.
(Essay)
4.8/5  (33)
(33)
A scatterplot showed a nonlinear relationship between y and an independent variable x. The x values were transformed using a square-root transformation, and a scatterplot of y versus 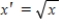 was approximately linear. The least squares regression line summarizing the relationship between y and x' was
was approximately linear. The least squares regression line summarizing the relationship between y and x' was 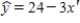 . What is the predicted value of y when
. What is the predicted value of y when 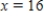 ?
?
(Multiple Choice)
5.0/5  (44)
(44)
Exhibit 4-7
Golden-rumped elephant shrews have long flexible snouts, used to overturn leaf-litter where they find their food: millipedes, insects and spiders. These animals are among the approximately 10% of mammalian species that mate for life. Just why these mammals are monogamous is poorly understood, and one theory is that a monogamous male would have to defend less territory from intrusion by other males. The home range of an animal, i.e. that area over which they typically travel, is a function of diet and energy consumption of the animal. The energy consumption is, in turn, typically a function of the animal's size. In a recent study, investigators reasoned that if monogamy was related in some way to the home territory, this should be detectable by comparing these animals to other insect-eating mammals. Data were gathered on 27 similar species and are presented in the table below. 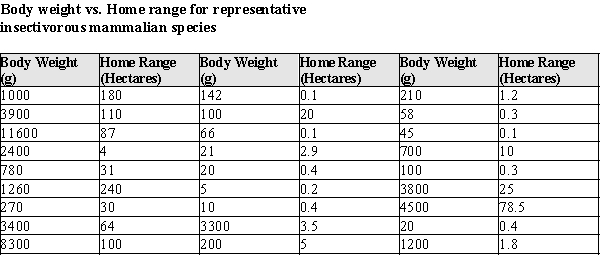 After fitting a straight line model,
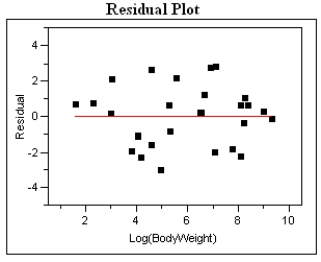
After fitting a straight line model, 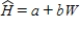 , significant curvature was detected in the residual plot, and two transformed models were chosen for further analysis: the power and exponential models. The computer output for these transformed models and the residual plots follow.
Residual Plot and Statistical Analysis - exponential model
, significant curvature was detected in the residual plot, and two transformed models were chosen for further analysis: the power and exponential models. The computer output for these transformed models and the residual plots follow.
Residual Plot and Statistical Analysis - exponential model 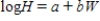
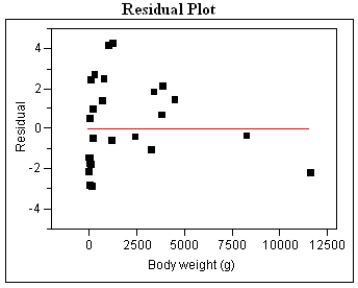 Log Home Range vs. Weight
Log(H) = 0.250 + 0.000231 W
Log Home Range vs. Weight
Log(H) = 0.250 + 0.000231 W  Residual Plot and Statistical Analysis - Power model
Residual Plot and Statistical Analysis - Power model 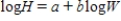
 Log Home Range vs. Log Weight
Log(H) = −1.601 + 0.893Log(W)
Log Home Range vs. Log Weight
Log(H) = −1.601 + 0.893Log(W)  -Refer to Exhibit 4-7. These shrews typically weigh 550g and their home range is about 2.9 hectares. Using your preferred model from part (c), locate the Golden-rumped elephant shrew on the appropriate residual plot by marking with a small "x." Does your placement of this point suggest the monogamy of these shrews sets them apart from similar species? In a few sentences, explain why or why not.
-Refer to Exhibit 4-7. These shrews typically weigh 550g and their home range is about 2.9 hectares. Using your preferred model from part (c), locate the Golden-rumped elephant shrew on the appropriate residual plot by marking with a small "x." Does your placement of this point suggest the monogamy of these shrews sets them apart from similar species? In a few sentences, explain why or why not.
(Essay)
4.8/5  (28)
(28)
Of the following, which is true of Pearson's correlation coefficient, r?
(Multiple Choice)
4.7/5  (36)
(36)
Showing 1 - 20 of 70
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)