Exam 13: Asking and Answering Questions About the Difference Between Two Means
Exam 1: Collecting Data in Reasonable Ways56 Questions
Exam 2: Graphical Methods for Describing Data Distributions62 Questions
Exam 3: Numerical Methods for Describing Data Distributions37 Questions
Exam 4: Describing Bivariate Numerical Data70 Questions
Exam 5: Probability55 Questions
Exam 6: Random Variables and Probability Distributions72 Questions
Exam 7: An Overview of Statistical Inference - Learning From Data19 Questions
Exam 8: Sampling Variability and Sampling Distributions35 Questions
Exam 9: Estimating a Population Proportion36 Questions
Exam 10: Asking and Answering Questions About a Population Proportion31 Questions
Exam 11: Asking and Answering Questions About the Difference Between Two Proportions42 Questions
Exam 12: Asking and Answering Questions About a Population Mean51 Questions
Exam 13: Asking and Answering Questions About the Difference Between Two Means46 Questions
Exam 14: Learning From Categorical Data36 Questions
Exam 15: Understanding Relationships - Numerical Data Part 243 Questions
Exam 16: Asking and Answering Questions About More Than Two Means25 Questions
Select questions type
Suppose that you wish to compare two treatments for preventing baldness in men. (The measure of baldness you will use is the mean number of healthy hair follicles per square cm.) In some circumstances, you may be able to randomly assign the treatments to the men, and in some circumstances, you may not be able to randomly assign the treatments to the men. Respond to the following questions in a few sentences.
a)If you are testing the hypothesis that the means are equal for the population, how would your statistical procedures differ, if at all, depending on whether you randomly assigned subjects to treatments or whether you merely observed differences in men who chose one treatment or the other?
b)How would your interpretation of the results differ, if at all, depending on whether you randomly assigned subjects to treatments or whether you merely observed differences in men who chose one treatment or the other?
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
a)The procedures for testing if the means are different for the two treatments would not differ. In each case a two sample t-test would be used.
b)The interpretation of the results would differ. If the subjects are randomly assigned to each of the treatments, then any statistically significant differences can be attributed to the different effect of the treatment. On the other hand, if the subjects have chosen the treatments, the difference might be due either to the treatments to some other unknown confounding variable, which affects the results.
When a surgeon repairs injuries, sutures (stitched knots) are sometimes used to hold together and stabilize the injured area. If these knots elongate and loosen, the injury may not heal properly. Researchers at the University of California, San Francisco, tied a particular type of knot with two types of suture material, Maxon and Ticron. Suppose that 112 tissue specimens were available and that for each specimen the type of suture material was randomly assigned. The investigators tested the knots to see how much they elongated. For purposes of this exercise, you can assume that it is reasonable to regard the elongation distributions as approximately normal. Which of the following hypotheses should be tested to determine if there is a significant difference in mean elongation between Maxon versus Ticron threads?
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
A
When testing a hypothesis concerning the difference of two independent population means, if the variance of the difference is estimated using the sample variances, the resulting test statistic has a Normal distribution.
Free
(True/False)
4.8/5  (35)
(35)
Correct Answer:
False
Suppose a researcher is collecting data to compare the average amount of soda consumed daily by men and women. The researcher will ask participants to state the amount of soda they consumed on the previous day. The researcher would like to determine if differences exist in the amount of soda consumed between the genders. Should the researcher use a procedure for two independent samples or paired data?
(Essay)
4.8/5  (37)
(37)
Does the gas leakage rate from automobile tires depend on the type of gas used to fill them?
A sample of automobile tires are filled with nitrogen to a pressure of 1 atmosphere, and the time is measured for the internal pressure to fall to 0.9 atmospheres. The experiment is repeated for this sample of tires, but using sulfur hexafluoride in place of nitrogen. The results are summarized below.  The null hypothesis is that the difference in mean population leak times is zero. Find the P-value for this test. Assume that the leakage times are normally distributed.
The null hypothesis is that the difference in mean population leak times is zero. Find the P-value for this test. Assume that the leakage times are normally distributed.
(Multiple Choice)
4.8/5  (38)
(38)
Viruses are infectious agents that often cause diseases in plants. Different viruses have different potency levels, and this fact can be used to detect whether a new virus is infecting plants in the field. In a potency comparison experiment, two viruses were placed on a tobacco leaf of 10 randomly selected tobacco plants in a field. The viruses were randomly assigned to one-half of each of the leaves. The table below presents the potency of the viruses, as measured by the number of lesions appearing on the leaf half.  Test the hypothesis that there is no difference in mean number of lesions for Virus X and Virus Y.
Test the hypothesis that there is no difference in mean number of lesions for Virus X and Virus Y.
(Essay)
4.8/5  (34)
(34)
When testing hypotheses about and constructing confidence intervals for μ1 − μ2, we utilize the statistic, 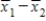 . What are the mean and variance of the sampling distribution of
. What are the mean and variance of the sampling distribution of 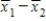 ?
?
(Essay)
4.7/5  (37)
(37)
Suppose 9 adult smokers were randomly selected. Researchers want to check whether the movie about the dangers of smoking affects the number of cigarettes smoked. The number of cigarettes per day before and after watching the movie was recorded for each smoker from the sample and resulting data are given in the accompanying table. 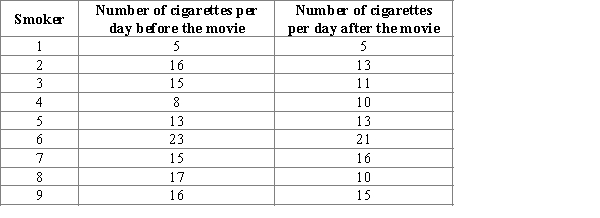 Select the most appropriate 95% bootstrap confidence interval for a difference in the mean number of cigarettes per day before and after watching the movie for adult smokers and its correct interpretation.
Select the most appropriate 95% bootstrap confidence interval for a difference in the mean number of cigarettes per day before and after watching the movie for adult smokers and its correct interpretation.
(Multiple Choice)
4.8/5  (33)
(33)
Suppose a researcher is testing a new diet drug. She would like to determine if the drug helps to significantly increase weight loss versus a placebo. She randomly assigns 40 participants to the treatment group and 35 to the placebo group. After 4 weeks on identical diets, the mean weights loss (in pounds) for each group is computed. Results of the study are as follows:
Treatment Group
Placebo Group
n = 40
n = 35  = 5.6
= 5.6  = 1.6
s = 2.85
s = 1.47
Perform a hypothesis test to draw a conclusion from this study. Show all your work.
= 1.6
s = 2.85
s = 1.47
Perform a hypothesis test to draw a conclusion from this study. Show all your work.
(Essay)
4.7/5  (26)
(26)
The large sample z test for μ1 − μ2 can be used as long as at least one of the two sample sizes, n1 and n2, is greater than or equal to 30.
(True/False)
5.0/5  (38)
(38)
In a recent paper, the authors distinguish between spending money on experiences (such as travel) and spending money on material possessions (such as a car). In an experiment to determine if the type of purchase affects how happy people are after the purchase has been made, 155 college students were randomly assigned to one of two groups. The students in the "experiential" group were asked to recall a time when they spent about $250 on an experience. They rated this purchase on three different happiness scales that were then combined into an overall measure of happiness. The students assigned to the "material" group recalled a time that they spent about $250 on an object and rated this purchase in the same manner. The mean happiness score was 5.62 for the experiential group and 5.44 for the material group.
Which of the following hypotheses should be tested to determine the author conclusion that, on average, "experiential purchases induced more reported happiness"?
(Multiple Choice)
4.7/5  (30)
(30)
A recent paper described an experiment in which 72 students at a university were assigned at random to one of two groups. All students took a class from the same instructor in the same semester. Students were required to report to an assigned room at a set time to fill out a course evaluation. One group of students reported to a room where they were offered a small bar of chocolate as they entered. The other group reported to a different room where they were not offered chocolate. Summary statistics for the overall course evaluation score are given in the accompanying table.  A 95% confidence interval for the mean difference in overall course evaluation score is:
A 95% confidence interval for the mean difference in overall course evaluation score is:
(Multiple Choice)
4.8/5  (39)
(39)
A common memory task is the classification of objects into categories. For example, a table is a piece of furniture; a dog is an animal, etc. This classification capability was used in a recent study of divided attention. Elderly adults were randomly selected from those answering a newspaper advertisement, and randomly assigned to two conditions: divided attention and no divided attention. Subjects in the "divided attention" group were told to memorize a list of 36 words while simultaneously listening to a tape recorder; subjects in a control group were told to memorize a list of 36 words and did not listen to a tape recorder. Subjects were then asked to classify the 36 words into 6 categories. (There were 6 words in each category.) The distributions of the correct number of recalled words / category were approximately normal in each of the groups, and a summary of the data for the words/category recalled are presented below: 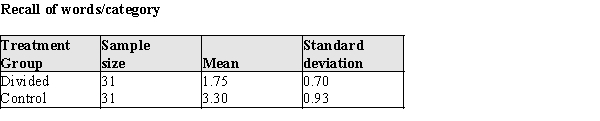
a)Is there evidence that the memory performance differs in the two groups? Test the appropriate hypothesis using α = .05.
b)One possible implication of this study is that high school students should not be dividing their attention by listening to music while studying. What results, if any, of this study would support the contention that students should not be dividing their attention?
a)Is there evidence that the memory performance differs in the two groups? Test the appropriate hypothesis using α = .05.
b)One possible implication of this study is that high school students should not be dividing their attention by listening to music while studying. What results, if any, of this study would support the contention that students should not be dividing their attention?
(Essay)
4.8/5  (31)
(31)
Researchers have hypothesized that female Downy Woodpeckers avoid the feeding areas of socially dominant males; that is, the males chase them away from prime spots. An alternative opinion is that there are important physical characteristics of males and females that might lead them to choose different foraging locations. One such characteristic could be the bill length of the males and females; it may be that longer bills let one gender or the other drill deeper into a tree and thus get more food per tree.
The data in the table below are the bill lengths of 12 male and 12 female randomly selected Downy Woodpeckers caught and released in a banding survey. The investigators would like to know whether these data provide evidence that the males and females differ in bill size. 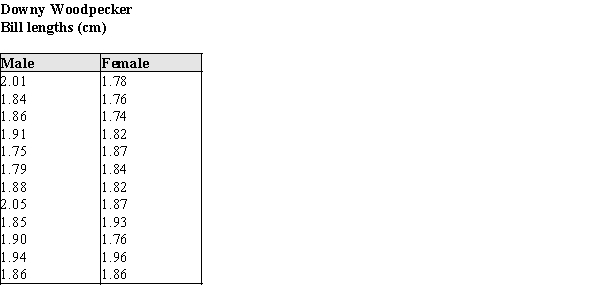
a)Using a graphical display of your choosing, assess the plausibility of the assumption that the distributions of bill lengths are approximately normal. State your conclusion in a few sentences.
b)Assuming that it is OK to proceed with a two-sample t procedure, determine if there is sufficient evidence to conclude that there is a difference in mean bill length for males and females.
c)In a few sentences, state any concerns you have about your conclusions in part (b), based on your results from part (a). If you have no concerns, write "No concerns."
a)Using a graphical display of your choosing, assess the plausibility of the assumption that the distributions of bill lengths are approximately normal. State your conclusion in a few sentences.
b)Assuming that it is OK to proceed with a two-sample t procedure, determine if there is sufficient evidence to conclude that there is a difference in mean bill length for males and females.
c)In a few sentences, state any concerns you have about your conclusions in part (b), based on your results from part (a). If you have no concerns, write "No concerns."
(Essay)
4.8/5  (39)
(39)
The home range of an animal is the average area an animal occupies while foraging for food and defending its territory. It is thought that home ranges of animals usually do not change much, except when an area is under ecological stress. As part of a study of white-tailed deer in Florida in 1991 and 1992, deer were radiocollared and their movements followed over the course of a year. The home range data for a random sample of 18 white-tailed deer are shown below in Table 1. The raw area of the home range for each of the deer is reported in hectares for the years 1991 and 1992. (A hectare is a metric unit of area equal to 2.471 acres.) The investigators are interested in determining whether the home range white-tailed deer change over the course of as little time as a year. 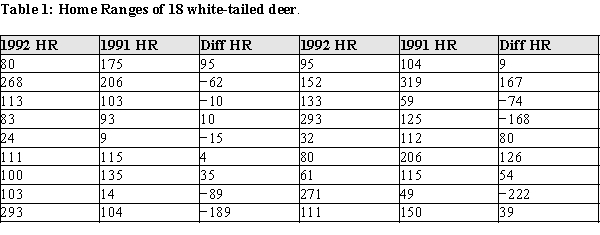
a)Using graphical display(s) of your choice show that the assumptions necessary for determining a change in the mean home ranges are plausible.
b)Construct a 95% confidence interval for the difference in means of the home ranges from 1991 to 1992.
c)Do the data provide evidence of a change in the size of the home ranges between 1991 and 1992? Provide statistical justification for y.
a)Using graphical display(s) of your choice show that the assumptions necessary for determining a change in the mean home ranges are plausible.
b)Construct a 95% confidence interval for the difference in means of the home ranges from 1991 to 1992.
c)Do the data provide evidence of a change in the size of the home ranges between 1991 and 1992? Provide statistical justification for y.
(Essay)
4.8/5  (42)
(42)
When testing hypotheses about and constructing confidence intervals for μ1 − μ2, we utilize the statistic, 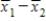 . What are the mean and standard deviation of the sampling distribution of
. What are the mean and standard deviation of the sampling distribution of 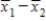 ?
?
(Essay)
4.9/5  (19)
(19)
A researcher investigates the effect of a new drug on resting heart rate.The resting heart rates of 15 patients are measured before and after administration of the drug. The results are summarized in the table below.  The question of interest is whether the resting heart rate increases after administration of the drug. Find the value of the test statistic.
The question of interest is whether the resting heart rate increases after administration of the drug. Find the value of the test statistic.
(Multiple Choice)
4.8/5  (28)
(28)
As part of the iguana risk assessment experiment described in the previous problem, investigators replicated the experiment with one difference--the investigators approached the iguanas at a tangent, passing by the iguana with a closest distance being 2 meters. Summary statistics for the approach distances for the two treatments, Eye Contact and No Eye Contact, are given in the table below: 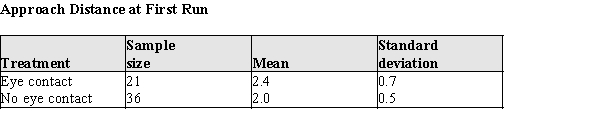 An initial analysis of the data revealed that it was reasonable to assume the population approach distances at first run were both approximately normal.
a)Construct a 95% confidence interval for the difference in approach distances for the eye contact and no eye contact treatments.
b)Do the data indicate that for a tangential approach, the population means differ? Justify your answer statistically.
An initial analysis of the data revealed that it was reasonable to assume the population approach distances at first run were both approximately normal.
a)Construct a 95% confidence interval for the difference in approach distances for the eye contact and no eye contact treatments.
b)Do the data indicate that for a tangential approach, the population means differ? Justify your answer statistically.
(Essay)
4.9/5  (40)
(40)
An article describes a study of the effectiveness of a fabric device that acts like a support stocking for a weak or damaged heart. In the study, 94 people who consented to treatment were assigned at random to either a standard treatment (S) consisting of drugs or the experimental treatment (E) that consisted of drugs plus surgery to install the stocking. After two years, 36% of the 61 patients receiving the stocking had improved,while 23% of the patients receiving the standard treatment had improved. Which of the following hypotheses should be tested to determine whether the proportion of patients who improve is significantly higher for the experimental treatment than for the standard treatment?
(Multiple Choice)
4.9/5  (39)
(39)
Showing 1 - 20 of 46
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)