The data below represent the numbers of absences and the final grades of 15 randomly selected students from a statistics class. Construct a scattergram for the data. Do you detect a trend? \[\begin{array}{l} \begin{array} { c c c } \text { Student}&\text { Number of Absences}&\text { Final Grade as a Percent }\\ 1 & 5 & 79 \\ 2 & 6 & 78 \\ 3 & 2 & 86 \\ 4 & 12 & 56 \\ 5 & 9 & 75 \\ 6 & 5 & 90 \\ 7 & 8 & 78 \\ 8 & 15 & 48 \\ 9 & 0 & 92 \\ 10 & 1 & 78 \\ 11 & 9 & 81 \\ 12 & 3 & 86 \\ 13 & 10 & 75 \\ 14 & 3 & 89 \\ 15 & 11 & 65 \end{array} \end{array}\]

@#IMG-DLM& There appears to be a trend i

The test scores of 30 students are listed below. Which number could be the 30th percentile? $\begin{array} { l l l l l l l l l l } 31 & 41 & 45 & 48 & 52 & 55 & 56 & 56 & 63 & 65 \end{array}$ $\begin{array} { l l l l l l l l l l } 67 & 67 & 69 & 70 & 70 & 74 & 75 & 78 & 79 & 79 \end{array}$ $\begin{array} { l l l l l l l l l l } 80 & 81 & 83 & 85 & 85 & 87 & 90 & 92 & 95 & 99 \end{array}$

A) 64 B) 56 C) 67 D) 90 A) 64 B) 56 C) 67 D) 90

The following is a list of 25 measurements: \[\begin{array} { l l l l l l l l l l l } 12 & 18 & 14 & 17 & 19 & 16 & 14 & 18 & 15 & 17 & 11 \\ 13 & 14 & 11 & 16 & 18 & 15 & 13 & 17 & 15 & 14 & 19 \\ 12 & 16 & 17 & & & & & & & & \end{array}\] How many of the measurements fall within one standard deviation of the mean?

A) 16 B) 18 C) 13 D) 25 A) 16 B) 18 C) 13 D) 25

Exam 2: Methods for Describing Sets of Data

A study was designed to investigate the effects of two variables - (1) a student's level of mathematical anxiety and (2) teaching method - on a student's achievement in a mathematics course. Students who had a low level of mathematical anxiety were taught using the traditional expository method. These students obtained a mean score of 470 with a standard deviation of 50 on a standardized test. Assuming a non-mound-shaped distribution, what percentage of the students scored over 620?

(Multiple Choice)

4.9/5

(37)

Question 61

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7 a. Explain why you cannot use the information in the table to construct a stem-and-leaf display for the data. b. Construct a histogram for the scores.

(Essay)

4.8/5

(37)

Question 62

The amount spent on textbooks for the fall term was recorded for a sample of five university students - $400, $350, $600, $525, and $450. Calculate the value of the sample median for the data.

(Multiple Choice)

4.8/5

(42)

Question 63

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Which statement following the table must be true? Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7

(Multiple Choice)

4.8/5

(40)

Question 64

The data below represent the numbers of absences and the final grades of 15 randomly selected students from a statistics class. Construct a scattergram for the data. Do you detect a trend? Student Number of Absences Final Grade as a Percent 1 5 79 2 6 78 3 2 86 4 12 56 5 9 75 6 5 90 7 8 78 8 15 48 9 0 92 10 1 78 11 9 81 12 3 86 13 10 75 14 3 89 15 11 65

(Essay)

4.9/5

(35)

Question 65

During one recent year, U.S. consumers redeemed 6.79 billion manufacturers' coupons and saved themselves $2.56 billion. Calculate and interpret the mean savings per coupon.

(Multiple Choice)

4.8/5

(33)

Question 66

Either vertical or horizontal bars can be used when constructing a bar graph.

(True/False)

4.7/5

(33)

Question 67

The mean x of a data set is 18, and the sample standard deviation s is 2. Explain what the interval (12, 24) represents.

(Essay)

4.7/5

(43)

Question 68

If a z-score is 0 or near 0, the measurement is located at or near the mean.

(True/False)

4.7/5

(39)

Question 69

252 randomly sampled college students were asked, among other things, to estimate their college grade point average (GPA). The responses are shown in the stem-and-leaf plot shown below. Notice that a GPA of 3.65 would be indicated with a stem of 36 and a leaf of 5 in the plot. How many of the students who responded had GPA's that exceeded 3.55? Stem and Leaf Plot of GPA 252 cases included

(Multiple Choice)

4.8/5

(45)

Question 70

The test scores of 30 students are listed below. Which number could be the 30th percentile? 31 41 45 48 52 55 56 56 63 65 67 67 69 70 70 74 75 78 79 79 80 81 83 85 85 87 90 92 95 99

(Multiple Choice)

4.7/5

(32)

Question 71

The following is a list of 25 measurements: 12 18 14 17 19 16 14 18 15 17 11 13 14 11 16 18 15 13 17 15 14 19 12 16 17 How many of the measurements fall within one standard deviation of the mean?

(Multiple Choice)

4.9/5

(38)

Question 72

Calculate the standard deviation of a sample for which $n = 6 , \sum x ^ { 2 } = 830 , \quad \sum { x } = 60$

(Multiple Choice)

4.9/5

(41)

Question 73

Test scores for a history class had a mean of 79 with a standard deviation of 4.5. Test scores for a physics class had a mean of 69 with a standard deviation of 3.7. One student earned a 86 on the history test and a 85 on the physics test. Calculate the z-score for each test. On which test did the student perform better?

(Essay)

4.8/5

(38)

Question 74

The mean of a data set is at the 50th percentile.

(True/False)

4.8/5

(39)

Question 75

The amount spent on textbooks for the fall term was recorded for a sample of five hundred university students. The mean expenditure was calculated to be $500 and the standard deviation of the expenditures was calculated to be $100. Suppose a randomly selected student reported that their textbook expenditure was $700. Calculate the z-score for this student's textbook expenditure.

(Multiple Choice)

4.9/5

(29)

Question 76

Which measures variability about the mean, the range or the standard deviation?

(Short Answer)

4.7/5

(39)

Question 77

A sample of professional golfers was taken and their driving distance (measured as the average distance as their drive off the tee) and driving accuracy (measured as the percentage of fairways that their drives landed in) were recorded. A scatterplot of the variables is shown below. 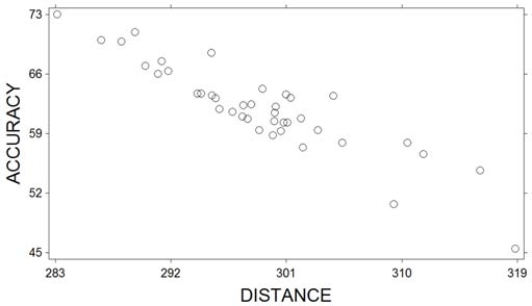What relationship do these two variables exhibit?

(Multiple Choice)

4.8/5

(32)

Question 78

The outer fences of a box plot are three standard deviations from the mean.

(True/False)

4.8/5

(38)

Question 79

A dot plot of the speeds of a sample of 50 cars passing a policeman with a radar gun is shown below. 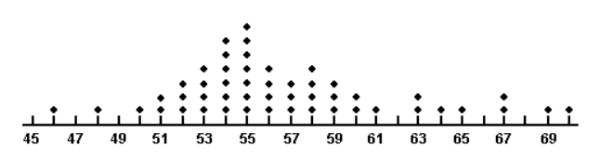What proportion of the motorists were driving above the posted speed limit of 60 miles per hour?

(Multiple Choice)

4.9/5

(43)

Question 80

The amount spent on textbooks for the fall term was recorded for a sample of five university students - $400, $350, $600, $525, and $450. Calculate the value of the sample median for the data.

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Which statement following the table must be true? Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7

During one recent year, U.S. consumers redeemed 6.79 billion manufacturers' coupons and saved themselves $2.56 billion. Calculate and interpret the mean savings per coupon.

Either vertical or horizontal bars can be used when constructing a bar graph.

The mean x of a data set is 18, and the sample standard deviation s is 2. Explain what the interval (12, 24) represents.

If a z-score is 0 or near 0, the measurement is located at or near the mean.

The test scores of 30 students are listed below. Which number could be the 30th percentile? 31 41 45 48 52 55 56 56 63 65 67 67 69 70 70 74 75 78 79 79 80 81 83 85 85 87 90 92 95 99

The following is a list of 25 measurements: 12 18 14 17 19 16 14 18 15 17 11 13 14 11 16 18 15 13 17 15 14 19 12 16 17 How many of the measurements fall within one standard deviation of the mean?

Calculate the standard deviation of a sample for which $n = 6 , \sum x ^ { 2 } = 830 , \quad \sum { x } = 60$

The mean of a data set is at the 50th percentile.

Which measures variability about the mean, the range or the standard deviation?

The outer fences of a box plot are three standard deviations from the mean.

A dot plot of the speeds of a sample of 50 cars passing a policeman with a radar gun is shown below. What proportion of the motorists were driving above the posted speed limit of 60 miles per hour?

Statistics, Data, and Statistical Thinking

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on a Single Sample: Tests of Hypothesis

Inferences Based on a Two Samples: Confidence Intervals and Tests of Hypotheses

Analysis of Variance: Comparing More Than Two Means

Simple Linear Regression

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics

Filters

Exam 2: Methods for Describing Sets of Data

The amount spent on textbooks for the fall term was recorded for a sample of five university students - $400, $350, $600, $525, and $450. Calculate the value of the sample median for the data.

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Which statement following the table must be true? Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7

During one recent year, U.S. consumers redeemed 6.79 billion manufacturers' coupons and saved themselves $2.56 billion. Calculate and interpret the mean savings per coupon.

Either vertical or horizontal bars can be used when constructing a bar graph.

The mean x of a data set is 18, and the sample standard deviation s is 2. Explain what the interval (12, 24) represents.

If a z-score is 0 or near 0, the measurement is located at or near the mean.

The test scores of 30 students are listed below. Which number could be the 30th percentile? 31 41 45 48 52 55 56 56 63 65 67 67 69 70 70 74 75 78 79 79 80 81 83 85 85 87 90 92 95 99

The following is a list of 25 measurements: 12 18 14 17 19 16 14 18 15 17 11 13 14 11 16 18 15 13 17 15 14 19 12 16 17 How many of the measurements fall within one standard deviation of the mean?

Calculate the standard deviation of a sample for which n=6,∑x2=830,∑x=60n = 6 , \sum x ^ { 2 } = 830 , \quad \sum { x } = 60n=6,∑x2=830,∑x=60

The mean of a data set is at the 50th percentile.

Which measures variability about the mean, the range or the standard deviation?

The outer fences of a box plot are three standard deviations from the mean.

A dot plot of the speeds of a sample of 50 cars passing a policeman with a radar gun is shown below. What proportion of the motorists were driving above the posted speed limit of 60 miles per hour?

Statistics, Data, and Statistical Thinking

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on a Single Sample: Tests of Hypothesis

Inferences Based on a Two Samples: Confidence Intervals and Tests of Hypotheses

Analysis of Variance: Comparing More Than Two Means

Simple Linear Regression

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics

Filters

Calculate the standard deviation of a sample for which $n = 6 , \sum x ^ { 2 } = 830 , \quad \sum { x } = 60$