Complete the frequency table for the data shown below. \[\begin{array}{l} \begin{array} { l l l l l } \text { green } & \text { blue } & \text { brown } & \text { orange } & \text { blue } \\ \text { brown } & \text { orange } & \text { blue } & \text { red } & \text { green } \\ \text { blue } & \text { brown } & \text { green } & \text { red } & \text { brown } \\ \text { blue } & \text { brown } & \text { blue } & \text { blue } & \text { red } \end{array}\\\\ \begin{array} { l | l } \text { Color } & \text { Frequency } \\ \hline \text { Green } & \\ \hline \text { Blue } & \\ \hline \text { Brown } & \\ \hline \text { Orange } & \\ \hline \end{array} \end{array}\]

The answer of Complete the frequency table for the data...

Exam 2: Methods for Describing Sets of Data

Complete the frequency table for the data shown below. green blue brown orange blue brown orange blue red green blue brown green red brown blue brown blue blue red Color Frequency Green Blue Brown Orange

(Essay)

4.8/5

(37)

Question 161

The calculator screens summarize a data set. 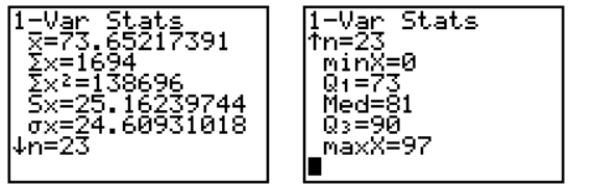a. Identify the mean and the median. b. Based only on the mean and the median, do you expect that the data set is skewed to the right, symmetric, or skewed to the left? Explain.

(Essay)

4.8/5

(35)

Question 162

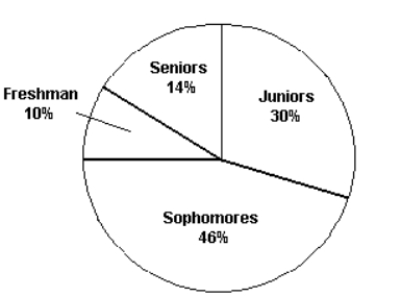The pie chart shows the classifications of students in a statistics class. What percentage of the class consists of freshman, sophomores, and juniors?

(Multiple Choice)

4.9/5

(31)

Question 163

In a summary of recent real estate sales, the median home price is given as $325,000. What percentile corresponds to a home price of $325,000?

(Short Answer)

4.8/5

(39)

Question 164

A recent survey was conducted to compare the cost of solar energy to the cost of gas or electric energy. Results of the survey revealed that the distribution of the amount of the monthly utility bill of a 3-bedroom house using gas or electric energy had a mean of $104 and a standard deviation of $10. If nothing is known about the shape of the distribution, what percentage of homes will have a monthly utility bill of less than $84?

(Multiple Choice)

4.9/5

(38)

Question 165

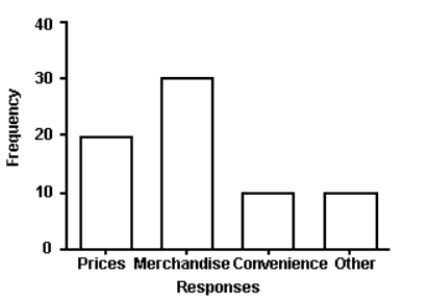$The manager of a store conducted a customer survey to determine why customers shopped at the store. The results are shown in the figure. What proportion of customers responded that merchandise was the reason they shopped at the store? A) \frac { 3 } { 7 } B) 30 C) \frac { 1 } { 2 } D) \frac { 2 } { 7 }$ The manager of a store conducted a customer survey to determine why customers shopped at the store. The results are shown in the figure. What proportion of customers responded that merchandise was the reason they shopped at the store? A) $\frac { 3 } { 7 }$ B) 30 C) $\frac { 1 } { 2 }$ D) $\frac { 2 } { 7 }$

(Short Answer)

4.9/5

(29)

Question 166

The calculator screens summarize a data set. 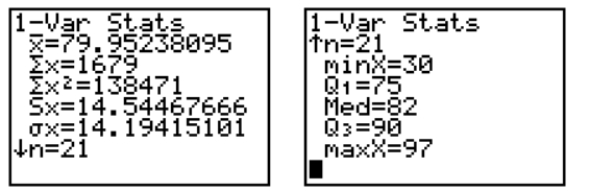a. Identify the smallest measurement in the data set. b. Identify the largest measurement in the data set. c. Calculate the range of the data set.

(Essay)

4.9/5

(35)

Question 167

On a given day, the price of a gallon of milk had a mean price of $2.30 with a standard deviation of $0.05. A particular food store sold milk for $2.25/gallon. Interpret the z-score for this gas station.

(Multiple Choice)

4.8/5

(32)

Question 168

In a symmetric and mound shaped distribution, we expect the values of the mean, median, and mode to differ greatly from one another.

(True/False)

4.8/5

(37)

Question 169

Explain how stretching the vertical axis of a histogram can be misleading.

(Essay)

4.9/5

(30)

Question 170

An outlier in a data set may have a simple explanation such as a scale was not working properly or the researcher inverted the digits of a number when recording a measurement.

(True/False)

4.8/5

(44)

Question 171

Explain how using a scale break on the vertical axis of a histogram can be misleading.

(Essay)

5.0/5

(35)

Question 172

In symmetric distributions, the mean and the median will be approximately equal.

(True/False)

4.9/5

(27)

Question 173

$\text { Compute } s ^ { 2 } \text { and } s \text { for the data set: } \frac { 1 } { 5 } , \frac { 3 } { 5 } , \frac { 1 } { 5 } , \frac { 1 } { 5 } , \frac { 1 } { 5 } , \frac { 1 } { 10 } \text {. }$

(Multiple Choice)

4.9/5

(32)

Question 174

A recent survey was conducted to compare the cost of solar energy to the cost of gas or electric energy. Results of the survey revealed that the distribution of the amount of the monthly utility bill of a 3-bedroom house using gas or electric energy had a mean of $135 and a standard deviation of $11. If the distribution can be considered mound-shaped and symmetric, what percentage of homes will have a monthly utility bill of more than $124?

(Multiple Choice)

4.8/5

(31)

Question 175

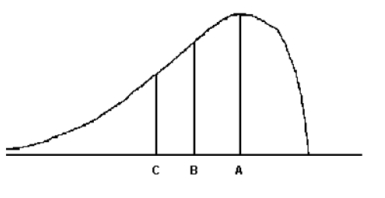$For the distribution drawn here, identify the mean, median, and mode. A) \mathrm { A } = mode, \mathrm { B } = median, \mathrm { C } = mean B) \mathrm { A } = median, \mathrm { B } = mode, \mathrm { C } = mean C) \mathrm { A } = mode, \mathrm { B } = mean, \mathrm { C } = median D) \mathrm { A } = mean, \mathrm { B } = mode, \mathrm { C } = median$ For the distribution drawn here, identify the mean, median, and mode. A) $\mathrm { A } =$ mode, $\mathrm { B } =$ median, $\mathrm { C } =$ mean B) $\mathrm { A } =$ median, $\mathrm { B } =$ mode, $\mathrm { C } =$ mean C) $\mathrm { A } =$ mode, $\mathrm { B } =$ mean, $\mathrm { C } =$ median D) $\mathrm { A } =$ mean, $\mathrm { B } =$ mode, $\mathrm { C } =$ median

(Short Answer)

4.9/5

(26)

Question 176

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Identify the modal class of the distribution of scores. Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7

(Essay)

4.9/5

(39)

Question 177

The amount of television viewed by today's youth is of primary concern to Parents Against Watching Television (PAWT). Three hundred parents of elementary school-aged children were asked to estimate the number of hours per week that their child watches television. The upper quartile for the distribution was given as 15 hours. Interpret this value.

(Essay)

4.9/5

(30)

Question 178

The amount of time workers spend commuting to their jobs each day in a large metropolitan city has a mean of 70 minutes and a standard deviation of 20 minutes. Assuming the distribution of commuting times is known to be moundshaped and symmetric, what percentage of these commuting times are between 50 and 110 minutes?

(Multiple Choice)

4.9/5

(34)

Question 179

Many firms use on-the-job training to teach their employees computer programming. Suppose you work in the personnel department of a firm that just finished training a group of its employees to program, and you have been requested to review the performance of one of the trainees on the final test that was given to all trainees. The mean and standard deviation of the test scores are 72 and 3, respectively, and the distribution of scores is mound-shaped and symmetric. Suppose the trainee in question received a score of 64 . Compute the trainee's z-score. A) $z = - 2.67$ B) $z = - 8$ C) $z = - 24$ D) $z = 0.85$

(Short Answer)

4.9/5

(26)

Question 180

Showing 161 - 180 of 194

Complete the frequency table for the data shown below. green blue brown orange blue brown orange blue red green blue brown green red brown blue brown blue blue red Color Frequency Green Blue Brown Orange

The calculator screens summarize a data set. a. Identify the mean and the median. b. Based only on the mean and the median, do you expect that the data set is skewed to the right, symmetric, or skewed to the left? Explain.

The pie chart shows the classifications of students in a statistics class. What percentage of the class consists of freshman, sophomores, and juniors?

In a summary of recent real estate sales, the median home price is given as $325,000. What percentile corresponds to a home price of $325,000?

The calculator screens summarize a data set. a. Identify the smallest measurement in the data set. b. Identify the largest measurement in the data set. c. Calculate the range of the data set.

On a given day, the price of a gallon of milk had a mean price of $2.30 with a standard deviation of $0.05. A particular food store sold milk for $2.25/gallon. Interpret the z-score for this gas station.

In a symmetric and mound shaped distribution, we expect the values of the mean, median, and mode to differ greatly from one another.

Explain how stretching the vertical axis of a histogram can be misleading.

An outlier in a data set may have a simple explanation such as a scale was not working properly or the researcher inverted the digits of a number when recording a measurement.

Explain how using a scale break on the vertical axis of a histogram can be misleading.

In symmetric distributions, the mean and the median will be approximately equal.

$\text { Compute } s ^ { 2 } \text { and } s \text { for the data set: } \frac { 1 } { 5 } , \frac { 3 } { 5 } , \frac { 1 } { 5 } , \frac { 1 } { 5 } , \frac { 1 } { 5 } , \frac { 1 } { 10 } \text {. }$

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Identify the modal class of the distribution of scores. Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7

Statistics, Data, and Statistical Thinking

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on a Single Sample: Tests of Hypothesis

Inferences Based on a Two Samples: Confidence Intervals and Tests of Hypotheses

Analysis of Variance: Comparing More Than Two Means

Simple Linear Regression

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics

Filters