Exam 3: Introduction to Logic
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Give the number of rows in the truth table for the compound statement.
-
(Multiple Choice)
4.8/5  (34)
(34)
Determine if the argument is valid or a fallacy. Give a reason to justify answer.
-If you eat well, you will be well.
If you eat well, you will be happy.
(Multiple Choice)
4.9/5  (31)
(31)
Use the method of writing each premise in symbols in order to write a conclusion that yields a valid argument.
-If I get robbed, I will go to court. I got robbed.
(Multiple Choice)
4.8/5  (36)
(36)
Convert the symbolic compound statement into words.
-p represents the statement "Her name is Lisa." q represents the statement "She lives in Chicago." Translate the following compound statement into words:
(Multiple Choice)
4.8/5  (43)
(43)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.9/5  (42)
(42)
Use a truth table to determine whether the argument is valid.
-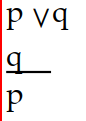
(Multiple Choice)
4.8/5  (29)
(29)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.8/5  (41)
(41)
Use an Euler diagram to determine whether the argument is valid or invalid.
-Some TV shows are comedies.
Some TV shows are hits.
(Multiple Choice)
4.9/5  (30)
(30)
Label the pair of statements as either contrary or consistent.
-She likes coffee. She likes tea.
(Multiple Choice)
4.9/5  (37)
(37)
Use a truth table to determine whether the argument is valid.
- p\rightarrow\simq q\rightarrow\simp p\veeq
(Multiple Choice)
4.9/5  (38)
(38)
Rewrite the statement in the form "if p, then q".
-Practice is necessary for making the team.
(Multiple Choice)
4.9/5  (36)
(36)
Write an equivalent statement that does not use the if ... then connec
-If you can't win the set, then you don't bother playing.
(Multiple Choice)
4.9/5  (38)
(38)
Rewrite the statement using the if...then connective. Rearrange the wording or words as necessary.
-A ship can't sail on land.
(Multiple Choice)
4.8/5  (30)
(30)
Write the converse, inverse, or contrapositive of the statement as requested.
-
Contrapositive
(Use one of De Morgan's laws)
(Multiple Choice)
4.9/5  (30)
(30)
Decide whether the statement is true or false.
-Every rational number is an integer.
(True/False)
4.8/5  (38)
(38)
Use the method of writing each premise in symbols in order to write a conclusion that yields a valid argument.
-Hard workers sweat. Sweat brings on a chill. Anyone who doesn't have a cold never felt a chill. Anyone who works doesn't have a cold.
(Multiple Choice)
4.8/5  (36)
(36)
Convert the symbolic compound statement into words.
-p represents the statement: " "
q represents the statement: " "
Translate the following compound statement into words:
(Multiple Choice)
4.8/5  (34)
(34)
Write a logical statement representing the following circuit. Simplify when possible.
-
(Essay)
4.9/5  (37)
(37)
Showing 281 - 300 of 315
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)