Exam 3: Introduction to Logic
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Label the pair of statements as either contrary or consistent.
-This number is greater than 20. This number is negative.
(Multiple Choice)
4.8/5  (33)
(33)
Write the converse, inverse, or contrapositive of the statement as requested.
-If you like me, then I like you. Converse
(Multiple Choice)
5.0/5  (33)
(33)
Solve the logic puzzle by using a grid.
-Five students, Cynthia, Paulene, Chris, Mary and Janet got colored paper. No two had the same color. The six colors were: red, orange, white, black, yellow and green. Cynthia got a bright color.
Janet and Paulene got similar colors. Chris didn't get red. Mary didn't get green. Neither Chris nor
Paulene got orange. Cynthia and Paulene's colors combine to make Janet's color. Mary got the
Darkest color. Chris did not get white. Match students and colors.
(Multiple Choice)
4.7/5  (38)
(38)
Tell whether the conditional statement is true or false.
-Here T represents a true statement.
(True/False)
4.9/5  (38)
(38)
The argument has a true conclusion. Identify the argument as valid or invalid.
-All soda pops are carbonated.
All diet colas are carbonated.
(Multiple Choice)
4.8/5  (28)
(28)
Write an equivalent statement that does not use the if ... then connec
-If your suit needs cleaning, you drop it off this afternoon.
(Multiple Choice)
4.8/5  (33)
(33)
Rewrite the statement using the if...then connective. Rearrange the wording or words as necessary.
-Cats chase mice.
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-Given that is false, what can you conclude about the truth values of and ?
(Multiple Choice)
4.8/5  (34)
(34)
Use an Euler diagram to determine whether the argument is valid or invalid.
-All painters use paint.
All painters use brushes.
Some painters are teachers.
(Multiple Choice)
4.8/5  (33)
(33)
Determine whether the argument is valid or invalid.
-Michael Bolton is a hunk or Madonna cannot sing. If Madonna cannot sing, then Cigar does not win the Triple Crown. Cigar wins the Triple Crown. Therefore, Michael Bolton is not a hunk.
(Multiple Choice)
4.8/5  (25)
(25)
Rewrite the statement in the form "if p, then q".
- only if .
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the argument is valid or invalid.
-If I hear that poem, it reminds me of my mother. If I get sentimental, then it does not remind me of my mother. I get sentimental. Therefore, I don't hear that poem.
(Multiple Choice)
4.8/5  (26)
(26)
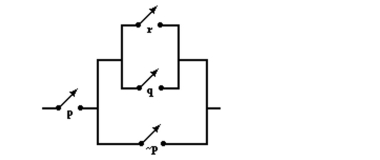
Write a logical statement representing the following circuit. Simplify when possible.
-
(Short Answer)
4.9/5  (32)
(32)
Use an Euler diagram to determine whether the argument is valid or invalid.
-All cats like fish.
Henry is not a cat.
(Multiple Choice)
4.7/5  (30)
(30)
Decide whether or not the following is a statement.
-This test is too hard.
(Multiple Choice)
4.7/5  (28)
(28)
Rewrite the statement using the if...then connective. Rearrange the wording or words as necessary.
-No turkeys like Thanksgiving.
(Multiple Choice)
4.7/5  (33)
(33)
Use the method of writing each premise in symbols in order to write a conclusion that yields a valid argument.
-Smiling people are happy. Alert people are not happy. Careful drivers are alert. Careless drivers have accidents.
(Multiple Choice)
4.9/5  (37)
(37)
Showing 141 - 160 of 315
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)