Exam 3: Introduction to Logic
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Write the converse, inverse, or contrapositive of the statement as requested.
-
Inverse
(Multiple Choice)
4.8/5  (36)
(36)
Let p represent a true statement and let q represent a false statement. Find the truth value of the given compound statement.
-
(True/False)
4.9/5  (32)
(32)
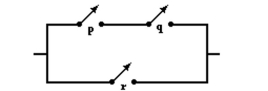
Write a logical statement representing the following circuit. Simplify when possible.
-
(Short Answer)
4.8/5  (32)
(32)
The argument has a true conclusion. Identify the argument as valid or invalid.
-Eric is older than Camille.
Todd is younger than Eric.
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the argument is valid or invalid.
-The Rams will be in the playoffs if and only if Ozzie is an all-star. Mark loves the Rams or Ozzie is an all-star. Mark does not love the Rams. Therefore, the Rams will not be in the playoffs.
(Multiple Choice)
4.8/5  (35)
(35)
Write a negation of the inequality. Do not use a slash symbol.
-
(Multiple Choice)
4.9/5  (36)
(36)
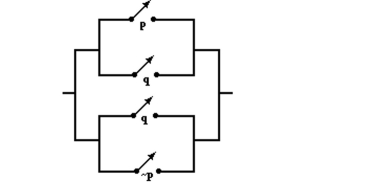
Write a logical statement representing the following circuit. Simplify when possible.
-
(Essay)
4.8/5  (38)
(38)
Use the method of writing each premise in symbols in order to write a conclusion that yields a valid argument.
-All birds have wings. None of my pets are birds. All animals with wings can flap them.
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-Given that is false, what can you conclude about the truth values of and ?
(Multiple Choice)
4.9/5  (35)
(35)
Write a negation for the statement.
-Not all people like football.
(Multiple Choice)
4.9/5  (26)
(26)
Use a truth table to determine whether the argument is valid.
- \rightarrow
(Multiple Choice)
4.9/5  (36)
(36)
Showing 261 - 280 of 315
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)