Exam 3: Introduction to Logic
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Determine whether the argument is valid or invalid.
-All women are wealthy. Amanda is a woman. Therefore, Amanda is wealthy.
(Multiple Choice)
4.7/5  (36)
(36)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.8/5  (35)
(35)
Decide whether the statement is compound.
-The sign read "Not for sale".
(Multiple Choice)
4.8/5  (30)
(30)
Let p represent a true statement and let q represent a false statement. Find the truth value of the given compound statement.
-
(True/False)
4.9/5  (29)
(29)
-If the package is in the mail, then it should be here by Tuesday.
(Multiple Choice)
4.8/5  (39)
(39)
Write a logical statement representing the following circuit. Simplify when possible.
-
(Essay)
4.8/5  (28)
(28)
Solve the logic puzzle by using a grid.
-Susan, Tim, Peter, Lucy and Norma have 20 pieces of candy to share. Susan only wants two pieces. Peter will take as many as he can. Tim and Lucy will end up with the same number of pieces.
Norma will not get the most pieces, but Susan will get the least pieces. Norma will get twice as
Many pieces as Susan and the same number as Tim. They all end up with an even number of pieces And no one has more than 10 pieces. How many pieces of candy does each get.
(Multiple Choice)
4.8/5  (31)
(31)
Write the compound statement in symbols. Let "The food is good."
p= "I eat too much." q= "I'll exercise."
-I'll exercise if I don't eat too much.
(Multiple Choice)
4.8/5  (40)
(40)
Solve the Sudoku.
-Easy 8 4 9 2 3 9 4 2 6 8 5 4 9 7 6 7 1 5 7 2 3 5 2 8 7 9 5 3 1 2 7 5 9 4 8 2
(Essay)
4.9/5  (31)
(31)
Write the converse, inverse, or contrapositive of the statement as requested.
-All cats catch birds. Inverse
(Multiple Choice)
4.8/5  (32)
(32)
Write a logical statement representing the following circuit. Simplify when possible.
-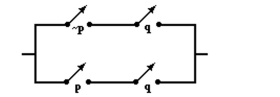
(Short Answer)
4.8/5  (35)
(35)
Decide whether the statement is true or false.
-For every real number r, r < 7 or r > 6.
(True/False)
4.7/5  (30)
(30)
Tell whether the conditional statement is true or false.
-Here T represents a true statement.
(True/False)
4.9/5  (34)
(34)
Give the number of rows in the truth table for the compound statement.
-
(Multiple Choice)
4.9/5  (32)
(32)
Use De Morgan's laws to write the negation of the statement.
-It is Saturday and it is not raining.
(Multiple Choice)
4.8/5  (37)
(37)
Write an equivalent statement that does not use the if ... then connec
-If the sun comes out Tuesday, the daisies will open.
(Multiple Choice)
4.7/5  (40)
(40)
Write the compound statement in words. Let "The puppy is trained."
"The puppy behaves well."
"His owners are happy."
-
(Multiple Choice)
4.9/5  (31)
(31)
Write the converse, inverse, or contrapositive of the statement as requested.
-
Converse
(Multiple Choice)
4.9/5  (36)
(36)
Use De Morgan's laws to write the negation of the statement.
-Roger or Emil will attend the game.
(Multiple Choice)
4.8/5  (36)
(36)
Showing 61 - 80 of 315
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)