Exam 3: Introduction to Logic
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Let p represent a true statement, while q and r represent false statements. Find the truth value of the compound statement.
-
(True/False)
4.8/5  (28)
(28)
Use De Morgan's laws to write the negation of the statement.
- and
(Multiple Choice)
4.7/5  (41)
(41)
Write the compound statement in words. Let "The puppy is trained."
"The puppy behaves well."
"His owners are happy."
-
(Multiple Choice)
4.8/5  (33)
(33)
Give the number of rows in the truth table for the compound statement.
-
(Multiple Choice)
4.7/5  (43)
(43)
Rewrite the statement in the form "if p, then q".
-Showing up at the party is sufficient to get a door prize.
(Multiple Choice)
4.9/5  (41)
(41)
Determine whether the argument is valid or invalid.
-If Cathy is a gambler, then she lives in Marine. Cathy lives in Marine and she loves horses. Therefore, if Cathy does not love horses, she is not a gambler.
(Multiple Choice)
5.0/5  (38)
(38)
Decide whether the statement is true or false.
-Not every whole number is a real number.
(True/False)
5.0/5  (39)
(39)
Rewrite the statement in the form "if p, then q".
-I will be happy only if he calls.
(Multiple Choice)
4.9/5  (35)
(35)
Rewrite the statement in the form "if p, then q".
-All numbers which are divisible by four are even numbers.
(Multiple Choice)
4.8/5  (25)
(25)
Convert the symbolic compound statement into words.
-p represents the statement : "Students are happy." q represents the statement: "Teachers are happy."
Translate the following compound statement into words:
(Multiple Choice)
4.9/5  (36)
(36)
Convert the symbolic compound statement into words.
-p represents the statement "It's raining in Chicago." q represents the statement "It's windy in Boston."
Translate the following compound statement into words:
(Multiple Choice)
4.8/5  (33)
(33)
Decide whether the compound statement is true or false. The symbol for exclusive disjunction represents "one or the other is true, but not both".
-
(True/False)
4.9/5  (33)
(33)
Decide whether or not the following is a statement.
-Not all flowers are roses.
(Multiple Choice)
4.8/5  (33)
(33)
Rewrite the statement using the if...then connective. Rearrange the wording or words as necessary.
-A ship can't sail on land.
(Multiple Choice)
4.8/5  (34)
(34)
Let p represent a true statement and let q represent a false statement. Find the truth value of the given compound statement.
-
(True/False)
4.7/5  (36)
(36)
Use a truth table to determine whether the argument is valid.
-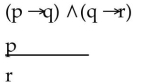
(Multiple Choice)
4.8/5  (31)
(31)
Showing 41 - 60 of 315
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)