Exam 3: Introduction to Logic
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Use a truth table to determine whether the argument is valid.
- \sim\rightarrow
(Multiple Choice)
4.9/5  (36)
(36)
Use the method of writing each premise in symbols in order to write a conclusion that yields a valid argument.
-All fish can dream. Any dead animal is unable to dream. All live animals have a heartbeat.
(Multiple Choice)
4.9/5  (36)
(36)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.8/5  (33)
(33)
Decide whether the statement is true or false.
-No rational number is not a whole number.
(True/False)
4.8/5  (27)
(27)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.9/5  (22)
(22)
Let p represent a true statement and let q represent a false statement. Find the truth value of the given compound statement.
-
(True/False)
4.9/5  (37)
(37)
Let p represent a true statement and let q represent a false statement. Find the truth value of the given compound statement.
-
(True/False)
5.0/5  (39)
(39)
Use the method of writing each premise in symbols in order to write a conclusion that yields a valid argument.
-Students who watch television while doing homework jeopardize their grades. Students with grades in jeopardy get grounded. Being grounded includes being barred from watching television.
(Multiple Choice)
4.7/5  (29)
(29)
Determine whether the argument is valid or invalid.
-If Ann so wishes, then Bill will be the president. Manuel is a public defender or Bill will be the president. Manuel is not a public defender. Therefore, Ann does not so wish.
(Multiple Choice)
4.8/5  (32)
(32)
Let p represent a true statement and let q represent a false statement. Find the truth value of the given compound statement.
-
(True/False)
4.9/5  (37)
(37)
Use a truth table to determine whether the argument is valid.
-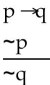
(Multiple Choice)
4.8/5  (37)
(37)
Write the converse, inverse, or contrapositive of the statement as requested.
-He who laughs last, laughs loudest. Inverse
(Multiple Choice)
4.9/5  (39)
(39)
Rewrite the statement using the if...then connective. Rearrange the wording or words as necessary.
-All children like stuffed toys.
(Multiple Choice)
5.0/5  (33)
(33)
Rewrite the statement using the if...then connective. Rearrange the wording or words as necessary.
-I have not accepted anyone who is from out of town.
(Multiple Choice)
4.8/5  (43)
(43)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.9/5  (42)
(42)
Showing 21 - 40 of 315
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)