Exam 4: Probability Concepts

Use the rule of total probability to find the indicated probability. -Among students at one college are 3874 women and 3058 men. The following table provides relative-frequency distributions for subject major for males and females at the college. Major Relative frequency for women Relative frequency for men Humanities 0.187 0.165 Science 0.284 0.349 Social Science 0.142 0.179 Other 0.387 0.307 A student is selected at random from the college. Determine the probability that the student is a Science major.

Use Bayes's rule to find the indicated probability. -Two shipments of components were received by a factory and stored in two separate bins. Shipment I has 2% of its contents defective, while shipment II has 5% of its contents defective. If it is Equally likely an employee will go to either bin and select a component randomly, what is the Probability that a defective component came from shipment II?

An experiment consists of randomly selecting a card from a deck of 52. The event A is defined as follows. A = event the card selected is a diamond Give an example of a pair of events B and C for this experiment such that the events A and B are mutually exclusive but the collection of events A, B, and C is not mutually exclusive.

Construct the joint probability distribution corresponding to the given contingency table. -The contingency table below provides a joint frequency distribution for a random sample of patients at a hospital classified by blood type and sex.

List the outcomes comprising the specified event. -When a quarter is tossed four times, 16 outcomes are possible. HHHH HHHT HHTH HHTT HTHH HTHT HTTH HTTT THHH THHT THTH THTT TTHH TTHT TTTH TTTT Here, for example, HTTH represents the outcome that the first toss is heads, the next two tosses are tails, and the fourth toss is heads. List the outcomes that comprise the following event. $\mathrm { A } =$ event exactly three tails are tossed

Use the basic counting rule to solve the problem. -License plates are made using 2 letters followed by 2 digits. How many plates can be made if repetition of letters and digits is allowed?

Determine whether the events are independent. -When a balanced die is rolled twice, 36 equally likely outcomes are possible. Let $\mathrm { A } =$ event the sum of the two rolls is 8 $B =$ event the first roll comes up 3 . Are A and B independent events?

Find the indicated probability. -A class consists of 54 women and 77 men. If a student is randomly selected, what is the probability that the student is a woman?

Use Bayes's rule to find the indicated probability. -The first two columns of the table below give a percentage distribution for adults in one city by income group. The third column gives the percentage of people in each income group who plan to Buy a new car next year. Income (dollars) Percentage of population Percentage that will buy new car next year 0-4999 5.2 2 5000-9999 6.4 3 10,000-14,999 5.4 6 15,000-19,999 8.7 7 20,000-24,999 9.4 9 25,000-29,999 10.2 10 30,000-34,999 13.8 11 35,000-39,999 10.7 13 40,000-49,999 15.5 15 50,000 and over 14.7 19 An adult is picked at random from the city. Given that the person selected plans to buy a new car Next year, what is the probability that the person's income is between $5,000 and $9,999?

Define mutually exclusive events and independent events. Give an example of each.

Describe an event whose probability of occurring is 1 and explain what that probability means. Describe an event whose probability of occurring is 0 and explain what that probability means.

Determine whether the events are independent. -An auto insurance company was interested in investigating accident rates for drivers in different age groups. The following contingency table was based on a random sample of drivers and Classifies drivers by age group and number of accidents in the past three years. 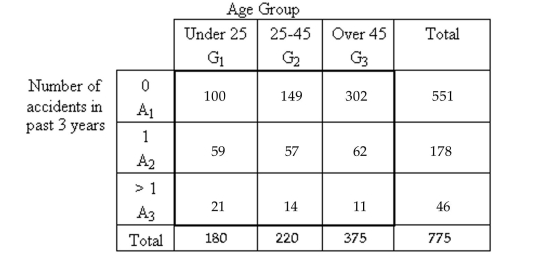Suppose that one of the drivers is selected at random. Are the events $\mathrm { G } _ { 1 }$ and $\mathrm { A } _ { 3 }$ independent?

Find the indicated probability by using the special addition rule. -The age distribution of students at a community college is given below. Age (years) Number of students (f) Under 21 406 21-25 419 26-30 205 31-35 60 Over 35 26 1116 A student from the community college is selected at random. Find the probability that the student is between 26 and 35 inclusive. Round approximations to three decimal places.

Use the basic counting rule to solve the problem. -A shirt company has 3 designs each of which can be made with short or long sleeves. There are 5 color patterns available. How many different types of shirts are available from this company?

Consider the following counting problem. Allison is trying to decide which three of her eight new books to take on vacation with her. How many different ways can she choose the three books? To solve this problem which of the following rules would you use?

Use Bayes's rule to find the indicated probability. -A person must select one of three boxes, each filled with clocks. The probability of box A being selected is 0.33, of box B being selected is 0.17, and of box C being selected is 0.5. The probability of Finding a red clock in box A is 0.2, in box B is 0.4, and in box C is 0.9. A box is selected. Given that The box contains a red clock, what is the probability that box A was chosen?

Provide an appropriate response. -A contingency table provides a joint frequency distribution for the popular votes cast in a presidential election by sex and political party. A joint probability distribution corresponding to the contingency table is obtained and can be represented as follows. 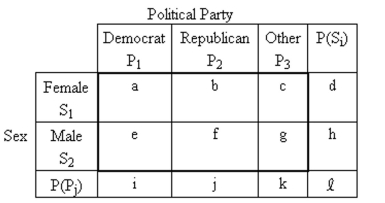The letters a through lare used to represent the probabilities in the different cells so, for example, the letter $f$ represents $P \left( P _ { 2 } \& S _ { 2 } \right)$ and the letter $h$ represents $P \left( S _ { 2 } \right)$ , $a + b + c = d$ ?

Use the special multiplication rule to find the indicated probability. -When a pair of dice is rolled there are 36 different possible outcomes: 1-1, 1-2, ... 6-6. If a pair of dice is rolled 3 times, what is the probability of getting a sum of 5 every time?

What important question must you answer before computing an "or" probability? How does the answer influence your computation?

On an exam question asking for a probability, Sue had an answer of $\frac { 13 } { 8 }$ . Explain how she knew that this result was incorrect.