Exam 4: Probability Concepts

List the outcomes comprising the specified event. -In a competition, two people will be selected from four finalists to receive the first and second prizes. The prize winners will be selected by drawing names from a hat. The names of the four Finalists are Jim, George, Helen, and Maggie. The possible outcomes can be represented as follows. JG JH JM GJ GH GM HJ HG HM MJ MG MH Here, for example, JG represents the outcome that Jim receives the first prize and George receives the second prize. The event $\mathrm { A }$ is defined as follows. $\mathrm { A } =$ event that Helen gets first prize List the outcomes that comprise the event (not A).

Suppose that S and T are mutually exclusive events. Which of the following statements is true?

Determine whether the events are independent. -The following contingency table provides a joint frequency distribution for a random sample of patients at a hospital classified by blood type and sex. 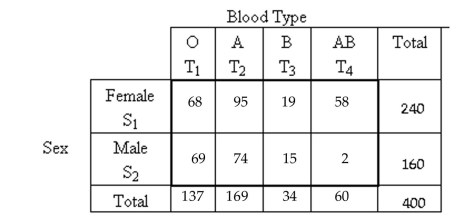Suppose one of the patients is selected at random. Are the events $\mathrm { T } _ { 2 }$ and $\mathrm { S } _ { 2 }$ independent?

Find the conditional probability. -If two fair dice are rolled, find the probability of a sum of 6 given that the roll is a "double".

Use counting rules to determine the probability. -A committee of 11 members is voting on a proposal. Each member casts a yea or nay vote. On a random voting basis, what is the probability that the proposal wins by a vote of 8 to 3?

Determine the number of outcomes that comprise the specified event. -The age distribution of students at a community college is given below. Age (years) Number of students (f) Under 21 2146 21-25 2027 26-30 1070 31-35 897 Over 35 200 A student from the community college is selected at random. The events A and B are defined as follows. A = event the student is between 21 and 35 inclusive B = event the student is 26 or over Determine the number of outcomes that comprise the event (A or B).

Explain why an event and its complement are always mutually exclusive and exhaustive.

The following contingency table provides a joint frequency distribution for the popular votes cast in the 1984 presidential election by region and political party. Data are in thousands, rounded to the nearest thousand. 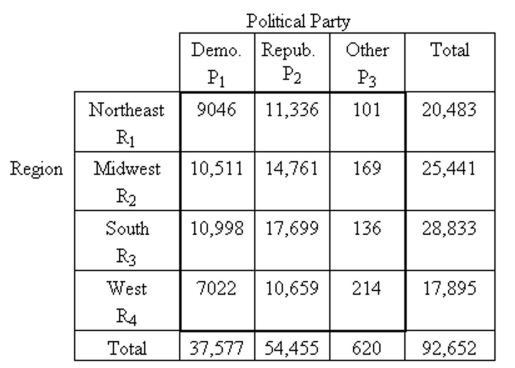If a person who voted in the 1984 presidential election is selected at random, $\mathrm { P } \left( \mathrm { R } _ { 2 } \& \mathrm { P } _ { 1 } \right) = 0.113$ . Interpret this probability in terms of percentages.

How many ways can 6 people be chosen and arranged in a straight line if there are 8 people to choose from?

A card is selected randomly from a standard deck of 52 cards. Let A = event that the card is an ace. Give examples of events B, C, and D such that A and B are independent, A and C are dependent but not mutually exclusive, and A and D are mutually exclusive.

$\text { Consider the following formulas: } ( n ) _ { r } = \frac { n ! } { ( n - r ) ! } \text { and } \left( \begin{array} { l } n \\ r \end{array} \right) = \frac { n ! } { ( n - r ) ! r ! } \text {. }$ Given the same values for n and r in each formula, which is the smaller value, P or C? How does this relate to the concept of counting the number of outcomes based on whether or not order is a criterion?

List the outcome(s)of the stated event. -The odds against winning in a horse race are shown in the following table. Horse \#1 \#2 \#3 \#4 \#5 \#6 \#7 Odds 8 15 2 22 12 15 22 Based on these odds, which horses comprise: A = event one of the top two favorites wins the race?

Use the rule of total probability to find the indicated probability. -A teacher designs a test so a student who studies will pass 82% of the time, but a student who does not study will pass 13% of the time. A certain student studies for 81% of the tests taken. On a given Test, what is the probability that student passes?

Draw a Venn diagram and shade the described events. -From a finite sample, events A, B, and C are mutually exclusive. Shade the collection A or B or C.

Use counting rules to determine the probability. -In a card game, each player is dealt 4 cards from an ordinary deck of 52 playing cards. Determine the probability of being dealt a hand containing three cards of one denomination and one of Another.

Determine the number of outcomes that comprise the specified event. -The number of hours needed by sixth grade students to complete a research project was recorded with the following results. Hours Number of students (f) 4 15 5 27 6 23 7 13 8 10 9 5 10+ 5 A student is selected at random. The events $A$ and $B$ are defined as follows. $A =$ the event the student took at most 8 hours $B =$ the event the student took at least 8 hours Determine the number of outcomes that comprise the event (A & B).

Provide an appropriate response. -A contingency table provides a joint frequency distribution for the popular votes cast in a presidential election by sex and political party. A joint probability distribution corresponding to the contingency table is obtained and can be represented as follows. 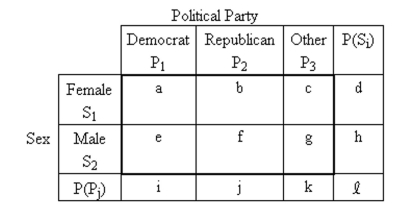The letters a through lare used to represent the probabilities in the different cells so, for example, the letter $\mathrm { f }$ represents $\mathrm { P } \left( \mathrm { P } _ { 2 } \& \mathrm {~S} _ { 2 } \right)$ and the letter h represents $\mathrm { P } \left( \mathrm { S } _ { 2 } \right)$ . if a person who voted in this election is selected at random, the events $\mathrm { P } _ { 2 }$ and $\mathrm { S } _ { 2 }$ are mutually exclusive?

Construct a Venn diagram portraying four events A, B, C, and D such that the collection of events A, B, and C is mutually exclusive, the collection of events A, B, and D is mutually exclusive, but the collection of events A, B, C, and D is not mutually exclusive.

Use the special multiplication rule to find the indicated probability. -A family has five children. The probability of having a girl is 1/2. What is the probability of having at least 4 girls?

List the outcomes comprising the specified event. -Three board members for a nonprofit organization will be selected from a group of five people. The board members will be selected by drawing names from a hat. The names of the five possible board Members are Allison, Betty, Charlie, Dave, and Emily. The possible outcomes can be represented as Follows. Here, for example, ABC represents the outcome that Allison, Betty, and Charlie are selected to be on the board. List the outcomes that comprise the following event. $A =$ event that fewer than two men are selected