Exam 4: Probability Concepts

Interpret the following probability statement using the frequentist interpretation of probability. The probability is 0.83 that this particular type of surgery will be successful.

If $\mathrm { P } ( \mathrm { A } ) = 0.25 , \mathrm { P } ( \mathrm { B } ) = 0.8$ , and $\mathrm { P } ( \mathrm { A } \& \mathrm {~B} ) = 0.23$ , are $\mathrm { A }$ and $\mathrm { B }$ independent events? How can you tell?

Find the indicated probability by using the special addition rule. -A card is drawn from a well-shuffled deck of 52 cards. What is the probability of drawing a face card or a 3?

List the outcomes comprising the specified event. -When a quarter is tossed four times, 16 outcomes are possible. HHHH HHHT HHTH HHTT HTHH HTHT HTTH HTTT THHH THHT THTH THTT TTHH TTHT TTTH TTTT Here, for example, HTTH represents the outcome that the first toss is heads, the next two tosses are tails, and the fourth toss is heads. List the outcomes that comprise the following event. $\mathrm { A } =$ event the last toss is heads

Find the indicated probability by using the complementation rule. -The distribution of B.A. degrees conferred by a local college is listed below, by major. Frequency English 2073 Mathematics 2164 Chemistry 318 Physics 856 Liberal Arts 1358 Business 1676 Engineering What is the probability that a randomly selected degree is not in Mathematics?

Use Bayes's rule to find the indicated probability. -34% of the workers at Motor Works are female, while 61% of the workers at City Bank are female. If one of these companies is selected at random (assume a 50-50 chance for each), and then a worker Is selected at random, what is the probability that the worker is female, given that the worker Comes from City Bank?

Solve the problem. -A poker hand consists of 5 cards dealt from an ordinary deck of 52 playing cards. How many different hands are there consisting of four hearts and one spade?

Use counting rules to determine the probability. -A tourist in France wants to visit 5 different cities. If the route is randomly selected, what is the probability that she will visit the cities in alphabetical order?

Find the conditional probability. -If a single fair die is rolled, find the probability of a 5 given that the number rolled is odd.

Find the indicated probability by using the general addition rule. -For a person selected randomly from a certain population, events A and B are defined as follows. A = event the person is male B = event the person is a smoker For this particular population, it is found that $\mathrm { P } ( \mathrm { A } ) = 0.47 , \mathrm { P } ( \mathrm { B } ) = 0.31$ , and $\mathrm { P } ( \mathrm { A } \& \mathrm {~B} ) = 0.12$ . Find $\mathrm { P } ( \mathrm { A }$ or $\mathrm { B } )$ . Round approximations to two decimal places.

Use Bayes's rule to find the indicated probability. -Among students at one college are 3936 women and 3197 men. The following table provides relative-frequency distributions for subject major for males and females at the college. Major Relative frequency for women Relative frequency for men Humanities 0.207 0.157 Science 0.299 0.354 Social Science 0.171 0.375 Other 0.323 0.114 A student is selected at random from the college. Determine the probability that the student Selected is female given that he or she is a Humanities major.

Solve the problem. -A poker hand consists of 5 cards dealt from an ordinary deck of 52 playing cards. How many different hands are there consisting of four cards of one suit and one card of another suit?

Interpret the symbol $\mathrm { P } ( \mathrm { B } \mid \mathrm { A } )$ and explain what is meant by the expression. What do we know if $P ( B \mid A )$ is not the same as $P ( B )$ ?

Use words or symbols, as indicated, to describe the event. -The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the Nearest thousand. 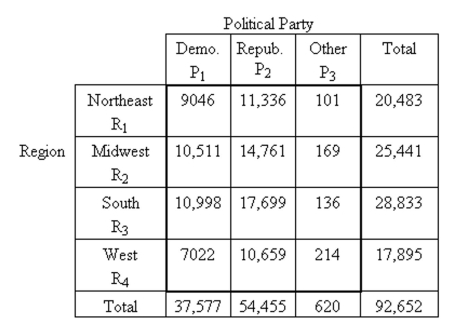Suppose a person who voted in the presidential election is selected at random. Describe in words the event $\left( R _ { 4 } \& P _ { 1 } \right)$ .

Use counting rules to determine the probability. -A student takes a true-false test consisting of 12 questions. Assuming that the student guesses at each question, find the probability that the student answers exactly 10 questions correctly.

Find the indicated probability. -If you flip a coin three times, the possible outcomes are HHH HHT HTH HTT THH THT TTH TTT. What is the probability of getting at least one head?

Discuss the differences, both in applications and in the formulas, for combinations and permutations. Give an example of each.

A relative frequency distribution is given below for the size of families in one U.S. city. Size Relative frequency 2 0.458 3 0.205 4 0.199 5 0.086 6 0.034 7+ 0.018 A family is selected at random. Find the probability that the size of the family is at most 6. Round approximations to three decimal places.

Suppose a student is taking a 5-response multiple choice exam; that is, the choices are A, B, C, D, and E, with only one of the responses correct. Describe the complement method for determining the probability of getting at least one of the questions correct on the 15-question exam. Why would the complement method be the method of choice for this problem?

List the outcome(s)of the stated event. -The odds against winning in a horse race are shown in the following table. Horse \#1 \#2 \#3 \#4 \#5 \#6 \#7 Odds 5 16 1 19 10 19 1 Based on these odds, which horses comprise: A = event the winning horse's number is above 4 ?