Question 1

Construct a Venn diagram representing the event $( ( A \& B ) \text { or } C )$

Accepted Answer

To construct a Venn diagram representing

Question 2

Draw a Venn diagram and shade the described events.
-From a finite sample, events A and B are mutually exclusive. Shade the collection A or B.

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 3

Suppose that in an election for governor of Oregon there are five candidates of whom two are women. A statistics student reasons as follows. The probability that a woman will win the election is equal to $\frac { \mathrm { f } } { \mathrm { N } }$ which is $\frac { 2 } { 5 }$. What is wrong with his reasoning?

Accepted Answer

The formula @#LAT-DLM& does no

Question 4

Construct a Venn diagram portraying three events A, B, and C such that A and B are
mutually exclusive, B and C are mutually exclusive, but the collection of events A, B, and C
is not mutually exclusive.

Accepted Answer

B
A ∩ B = ∅

B : C
B ∩ C = ∅

A : B : C

Question 5

An experiment consists of randomly selecting a card from a deck of 52. The event A is defined as follows.
A = event the card selected is a diamond
Give an example of an event B for this experiment such that the events A and B are mutually exclusive.

Accepted Answer

An example of an event B that would be m

Question 6

Discuss the range of possible values for probabilities. Give examples to support each.

Accepted Answer

Probabilities range between 0 and 1. P(A

Question 7

The age distribution of students at a community college is given below. $\begin{array}{lc}
\text { Age (years) } & \text { Number of students (f) } \
\hline \text { Under 21 } & 412 \
21-24 & 416 \
25-28 & 274 \
29-32 & 157 \
33-36 & 103 \
37-40 & 54 \
\text { Over 40 } & 95 \
\hline & 1511
\end{array}$
 A student from the community college is selected at random. Find the probability that the student is under 37 years old. Give your answer as a decimal rounded to three decimal places.

Accepted Answer

A) 0.099 
B) 0.901 
C) 0.036 
D) 0.068 
A) 0.099 
B) 0.901 
C) 0.036 
D) 0.068

Question 8

In a certain lottery, 4 numbers between 1 and 11 inclusive are drawn. These are the winning numbers. How many different selections are possible? Assume that the order in which the numbers Are drawn is not important.

Accepted Answer

A) 14,641 
B) 24 
C) 7920 
D) 330 
A) 14,641 
B) 24 
C) 7920 
D) 330

Question 9

Consider the following counting problem. A pool of possible jurors consists of 11 men and 13 women. How many different juries consisting of 5 women and 7 men are possible?
To solve this problem, which of the following rules would you use?

Accepted Answer

A) Both the combinations rule and the basic counting rule 
B) The combinations rule only 
C) Both the permutations rule and the basic counting rule 
D) The basic counting rule only 
A) Both the combinations rule and the basic counting rule 
B) The combinations rule only 
C) Both the permutations rule and the basic counting rule 
D) The basic counting rule only

Question 10

Use counting rules to determine the probability.
-8 basketball players are to be selected to play in a special game. The players will be selected from a list of 27 players. If the players are selected randomly, what is the probability that the 8 tallest Players will be selected?

Accepted Answer

A)  $\frac { 8 } { 27 }$ 
B)  $\frac { 1 } { 2,220,075 }$ 
C)  $\frac { 1 } { 213,127,200 }$ 
D)  $\frac { 1 } { 40,320 }$ 
A)  $\frac { 8 } { 27 }$ 
B)  $\frac { 1 } { 2,220,075 }$ 
C)  $\frac { 1 } { 213,127,200 }$ 
D)  $\frac { 1 } { 40,320 }$

Question 11

Find the conditional probability.
-The following contingency table provides a joint frequency distribution for the popular votes cast in the 1984 presidential election by region and political party. Data are in thousands, rounded to the Nearest thousand. 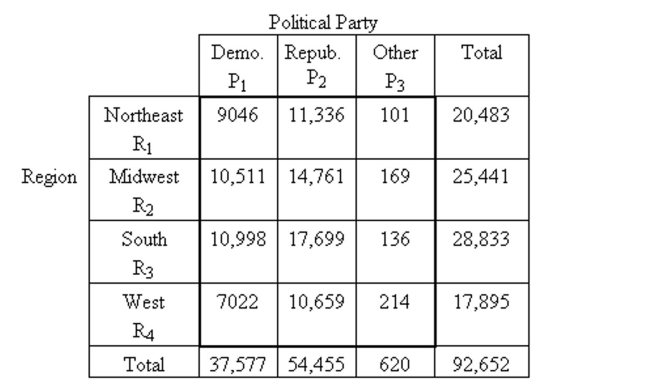  A person who voted in the 1984 presidential election is selected at random. Compute the Probability that the person selected voted Democrat given that they were in the Northeast.

Accepted Answer

A) 0.098 
B) 0.406 
C) 0.241 
D) 0.442 
A) 0.098 
B) 0.406 
C) 0.241 
D) 0.442

Question 12

Use Bayes's rule to find the indicated probability.
-Two stores sell a certain product. Store A has 40% of the sales, 3% of which are of defective items, and store B has 60% of the sales, 5% of which are of defective items. The difference in defective
Rates is due to different levels of pre-sale checking of the product. A person receives a defective Item of this product as a gift. What is the probability it came from store B?

Accepted Answer

A) 0.75 
B) 0.3 
C) 0.2857 
D) 0.7143 
A) 0.75 
B) 0.3 
C) 0.2857 
D) 0.7143

Question 13

List the outcomes comprising the specified event.
-Three board members for a nonprofit organization will be selected from a group of five people. The board members will be selected by drawing names from a hat. The names of the five possible board Members are Allison, Bob, Charlie, Dave, and Emily. The possible outcomes can be represented as Follows.
 $\begin{array}{lllll}
\mathrm{ABC} & \mathrm{ABD} & \mathrm{ABE} & \mathrm{ACD} & \mathrm{ACE} \
\mathrm{ADE} & \mathrm{BCD} & \mathrm{BCE} & \mathrm{BDE} & \mathrm{CDE}
\end{array}$

Here, for example, ABC represents the outcome that Allison, Bob, and Charlie are selected to be on the board. The events $A$ and $B$ are defined as follows.
$A =$ event that Dave is selected
$B =$ event that fewer than two men are selected
List the outcomes that comprise the event (A & B).

Accepted Answer

A) ABD, ADE, BDE, BCD, ACD, CDE 
B)  $\mathrm { ABD } , \mathrm { ADE } , \mathrm { BDE } , \mathrm { ABC } , \mathrm { ACE } , \mathrm { BCE }$ 
C)  $\mathrm { ABD } , \mathrm { ADE } , \mathrm { BDE }$ 
D)  $\mathrm { ABE } , \mathrm { ABD } , \mathrm { ADE } , \mathrm { BDE }$ 
A) ABD, ADE, BDE, BCD, ACD, CDE 
B)  $\mathrm { ABD } , \mathrm { ADE } , \mathrm { BDE } , \mathrm { ABC } , \mathrm { ACE } , \mathrm { BCE }$ 
C)  $\mathrm { ABD } , \mathrm { ADE } , \mathrm { BDE }$ 
D)  $\mathrm { ABE } , \mathrm { ABD } , \mathrm { ADE } , \mathrm { BDE }$

Question 14

Determine whether the events are independent.
-When a coin is tossed three times, eight equally likely outcomes are possible. 
HHH HHT HTH HTT
THH THT TTH TTT
Let
$A =$ event the first two tosses are the same
$B =$ event the total number of heads is one.
Are $A$ and $B$ independent events?

Accepted Answer

A) True 
 B)False

Question 15

Find the indicated probability by using the special addition rule.
-A percentage distribution is given below for the size of families in one U.S. city. 
$\begin{array} { l c } 
\text { Size } & \text { Percentage } \
\hline 2 & 49.6 \
3 & 24.6 \
4 & 13.4 \
5 & 7.3 \
6 & 3.1 \
7 + & 2.0
\end{array}$ 
A family is selected at random. Find the probability that the size of the family is at most 3. Round approximations to three decimal places.

Accepted Answer

A) 0.742 
B) 0.258 
C) 0.246 
D) 0.496 
A) 0.742 
B) 0.258 
C) 0.246 
D) 0.496

Question 16

Find the indicated probability by using the general addition rule.
-The manager of a bank recorded the amount of time each customer spent waiting in line during peak business hours one Monday. The frequency table below summarizes the results. 
$\begin{array}{l}
\text { Waiting Time Number of }\
\begin{array} { c | c } 
\text { (minutes) } & \text { Customers } \
\hline 0 - 3 & 10 \
4 - 7 & 15 \
8 - 11 & 15 \
12 - 15 & 8 \
16 - 19 & 7 \
20 - 23 & 2 \
24 - 27 & 2
\end{array}
\end{array}$ 
If we randomly select one of the times represented in the table, what is the probability that it is at Least 12 minutes or between 8 and 15 minutes?

Accepted Answer

A) 0.712 
B) 0.136 
C) 0.719 
D) 0.576 
A) 0.712 
B) 0.136 
C) 0.719 
D) 0.576

Question 17

Consider the following counting problem. Eight women and seven men are waiting in line at a movie theater. How many ways are there to arrange these 15 people amongst themselves such that
The eight women occupy the first eight places and the seven men the last seven places?
To solve this problem, which of the following rules would you use?

Accepted Answer

A) Both the combinations rule and the basic counting rule 
B) The basic counting rule only 
C) The permutations rule only 
D) Both the permutations rule and the basic counting rule 
A) Both the combinations rule and the basic counting rule 
B) The basic counting rule only 
C) The permutations rule only 
D) Both the permutations rule and the basic counting rule

Question 18

Use counting rules to determine the probability.
-Dave puts a collection of 15 books on a bookshelf in a random order. Among the books are 2 fiction and 13 nonfiction books. What is the probability that the 2 fiction books will be all together on the Left side of the shelf and the 13 nonfiction all together on the right side of the shelf?

Accepted Answer

A) 0.00952 
B) 0.01809 
C) 0.01333 
D) 0.01619 
A) 0.00952 
B) 0.01809 
C) 0.01333 
D) 0.01619

Question 19

Determine whether the events are independent.
-The following contingency table provides a joint probability distribution for a random sample of patients at a hospital classified by blood type and Sex.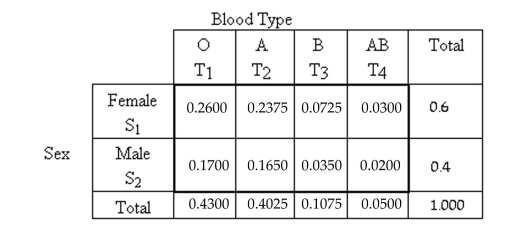

Suppose one of the patients is selected at random. Are the events $\mathrm { T } _ { 4 }$ and $\mathrm { S } _ { 1 }$ independent?

Accepted Answer

A) True 
 B)False

Question 20

Describe the specified event in words.
-The number of hours needed by sixth grade students to complete a research project was recorded with the following results. $$\begin{array} { r r } 
\text { Hours } & \text { Number of students (f) } \
\hline 4 & 15 \
5 & 11 \
6 & 19 \
7 & 6 \
8 & 9 \
9 & 16 \
10 & 2
\end{array}$$ A student is selected at random. The event A is defined as follows.
A = the event the student took at least 6 hours
Describe the event (not A) in words.

Accepted Answer

A) The event the student took at most 6 hours in words. 
B) The event the student did not take 6 hours 
C) The event the student took more than 6 hours 
D) The event the student took less than 6 hours 
A) The event the student took at most 6 hours in words. 
B) The event the student did not take 6 hours 
C) The event the student took more than 6 hours 
D) The event the student took less than 6 hours

Construct a Venn diagram representing the event $( ( A \& B ) \text { or } C )$

Draw a Venn diagram and shade the described events. -From a finite sample, events A and B are mutually exclusive. Shade the collection A or B.

Construct a Venn diagram portraying three events A, B, and C such that A and B are mutually exclusive, B and C are mutually exclusive, but the collection of events A, B, and C is not mutually exclusive.

An experiment consists of randomly selecting a card from a deck of 52. The event A is defined as follows. A = event the card selected is a diamond Give an example of an event B for this experiment such that the events A and B are mutually exclusive.

Discuss the range of possible values for probabilities. Give examples to support each.

In a certain lottery, 4 numbers between 1 and 11 inclusive are drawn. These are the winning numbers. How many different selections are possible? Assume that the order in which the numbers Are drawn is not important.

Consider the following counting problem. A pool of possible jurors consists of 11 men and 13 women. How many different juries consisting of 5 women and 7 men are possible? To solve this problem, which of the following rules would you use?

Use counting rules to determine the probability. -8 basketball players are to be selected to play in a special game. The players will be selected from a list of 27 players. If the players are selected randomly, what is the probability that the 8 tallest Players will be selected?

Determine whether the events are independent. -When a coin is tossed three times, eight equally likely outcomes are possible. HHH HHT HTH HTT THH THT TTH TTT Let $A =$ event the first two tosses are the same $B =$ event the total number of heads is one. Are $A$ and $B$ independent events?

The Nature of Statistics

Organizing Data

Descriptive Measures

Discrete Random Variables

The Normal Distribution

The Sampling Distribution of the Sample Mean

Confidence Intervals for One Population Mean

Hypothesis Tests for One Population Mean

Inferences for Two Population Means

Inferences for Population Standard Deviations

Inferences for Population Proportions

Chi-Square Procedures

Descriptive Methods in Regression and Correlation

Inferential Methods in Regression and Correlation

Analysis of Variance Anova

Filters

Exam 4: Probability Concepts

Construct a Venn diagram representing the event ((A&B) or C)( ( A \& B ) \text { or } C )((A&B) or C)

Draw a Venn diagram and shade the described events. -From a finite sample, events A and B are mutually exclusive. Shade the collection A or B.

Construct a Venn diagram portraying three events A, B, and C such that A and B are mutually exclusive, B and C are mutually exclusive, but the collection of events A, B, and C is not mutually exclusive.

An experiment consists of randomly selecting a card from a deck of 52. The event A is defined as follows. A = event the card selected is a diamond Give an example of an event B for this experiment such that the events A and B are mutually exclusive.

Discuss the range of possible values for probabilities. Give examples to support each.

In a certain lottery, 4 numbers between 1 and 11 inclusive are drawn. These are the winning numbers. How many different selections are possible? Assume that the order in which the numbers Are drawn is not important.

Consider the following counting problem. A pool of possible jurors consists of 11 men and 13 women. How many different juries consisting of 5 women and 7 men are possible? To solve this problem, which of the following rules would you use?

Use counting rules to determine the probability. -8 basketball players are to be selected to play in a special game. The players will be selected from a list of 27 players. If the players are selected randomly, what is the probability that the 8 tallest Players will be selected?

Determine whether the events are independent. -When a coin is tossed three times, eight equally likely outcomes are possible. HHH HHT HTH HTT THH THT TTH TTT Let A=A =A= event the first two tosses are the same B=B =B= event the total number of heads is one. Are AAA and BBB independent events?

The Nature of Statistics

Organizing Data

Descriptive Measures

Discrete Random Variables

The Normal Distribution

The Sampling Distribution of the Sample Mean

Confidence Intervals for One Population Mean

Hypothesis Tests for One Population Mean

Inferences for Two Population Means

Inferences for Population Standard Deviations

Inferences for Population Proportions

Chi-Square Procedures

Descriptive Methods in Regression and Correlation

Inferential Methods in Regression and Correlation

Analysis of Variance Anova

Filters

Construct a Venn diagram representing the event $( ( A \& B ) \text { or } C )$

Determine whether the events are independent. -When a coin is tossed three times, eight equally likely outcomes are possible. HHH HHT HTH HTT THH THT TTH TTT Let $A =$ event the first two tosses are the same $B =$ event the total number of heads is one. Are $A$ and $B$ independent events?